In my previous posts, I used the read_stata() method to read Stata datasets into pandas data frames. This works well when you want to read an entire Stata dataset into Python. But sometimes we wish to read a subset of the variables or observations, or both, from a Stata dataset into Python. In this post, I will introduce you to the Stata Function Interface (SFI) module and show you how to use it to read partial datasets into a pandas data frame. Read more…

Machine learning, deep learning, and artificial intelligence are a collection of algorithms used to identify patterns in data. These algorithms have exotic-sounding names like “random forests”, “neural networks”, and “spectral clustering”. In this post, I will show you how to use one of these algorithms called a “support vector machines” (SVM). I don’t have space to explain an SVM in detail, but I will provide some references for further reading at the end. I am going to give you a brief introduction and show you how to implement an SVM with Python.

Our goal is to use an SVM to differentiate between people who are likely to have diabetes and those who are not. We will use age and HbA1c level to differentiate between people with and without diabetes. Age is measured in years, and HbA1c is a blood test that measures glucose control. The graph below displays diabetics with red dots and nondiabetics with blue dots. An SVM model predicts that older people with higher levels of HbA1c in the red-shaded area of the graph are more likely to have diabetes. Younger people with lower HbA1c levels in the blue-shaded area are less likely to have diabetes. Read more…

Data are everywhere. Many government agencies, financial institutions, universities, and social media platforms provide access to their data through an application programming interface (API). APIs often return the requested data in a JavaScript Object Notation (JSON) file. In this post, I will show you how to use Python to request data with API calls and how to work with the resulting JSON data. Read more…

In my first four posts about Stata and Python, I showed you how to set up Stata to use Python, three ways to use Python in Stata, how to install Python packages, and how to use Python packages. It might be helpful to read those posts before you continue with this post if you are not familiar with Python. Now, I’d like to shift our focus to some practical uses of Python within Stata. This post will demonstrate how to use Stata to estimate marginal predictions from a logistic regression model and use Python to create a three-dimensional surface plot of those predictions.

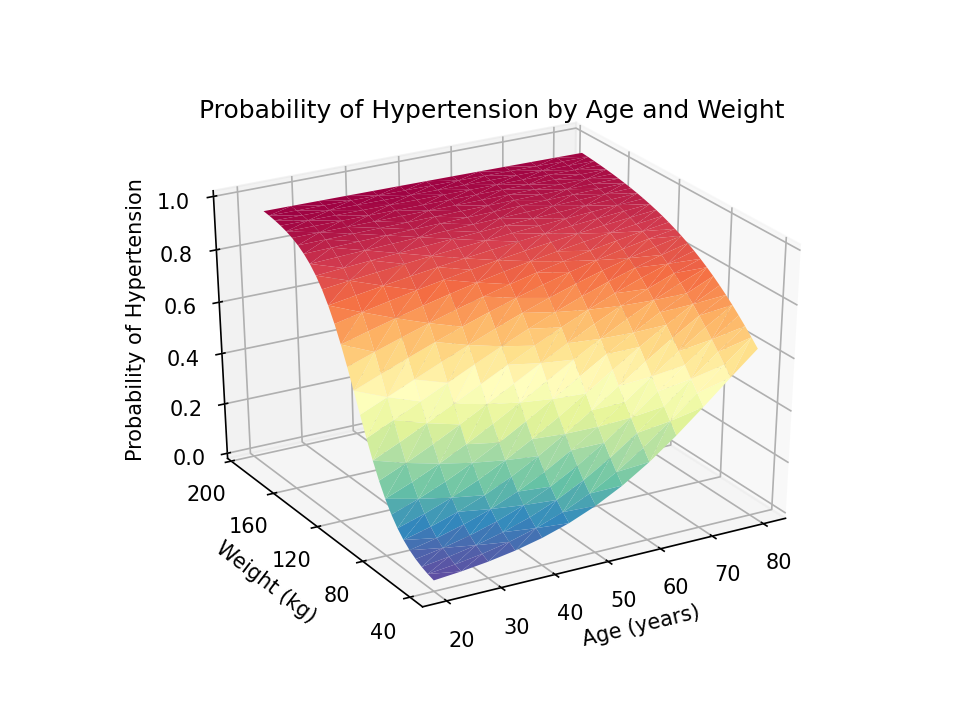
Read more…

In my last post, I showed you how to use pip to install four popular packages for Python. Today I want to show you the basics of how to import and use Python packages. We will learn some important Python concepts and jargon along the way. I will be using the pandas package in the examples below, but the ideas and syntax are the same for other Python packages. Read more…

In my last post, I showed you three ways to use Python within Stata. The examples were simple but they allowed us to start using Python. At this point, you could write your own Python programs within Stata. But the real power of Python lies in the thousands of freely available packages. Today, I want to show you how to download and install Python packages. Read more…

In my last post, I showed you how to install Python and set up Stata to use Python. Now, we’re ready to use Python. There are three ways to use Python within Stata: calling Python interactively, including Python code in do-files and ado-files, and executing Python script files. Each is useful in different circumstances, so I will demonstrate all three. The examples are intentionally simple and somewhat silly. I’ll show you some more complex examples in future posts, but I want to keep things simple in this post. Read more…

Python integration is one of the most exciting features in Stata 16. There are thousands of free Python packages that you can use to access and process data from the Internet, visualize data, explore data using machine-learning algorithms, and much more. You can use these Python packages interactively within Stata or incorporate Python code into your do-files. And there are a growing number of community-contributed commands that have familiar, Stata-style syntax that use Python packages as the computational engine. But there are a few things that we must do before we can use Python in Stata. This blog post will show you how to set up Stata to use Python. Read more…

Apple recently announced that it will be transitioning from Intel processors to its own ARM architecture processors currently being called Apple Silicon. Stata has a long history of supporting Macs, which includes the transitions from Motorola to PowerPC processors, from MacOS Classic to MacOS X, and from PowerPC to Intel processors. We will be working to support the new Macs as they transition from Intel processors to Apple Silicon and will continue our support of Macs with Intel processors as well.

Stata Press is pleased to announce the release of Data Management Using Stata: A Practical Handbook, Second Edition by Michael N. Mitchell.

Whether you are a new user needing to import, clean, and prepare data for your first analysis in Stata or you are an experienced user hoping to learn new tricks for the most challenging tasks, this book is for you. You can jump straight to the section of the book that discusses the particular challenge you are facing. There you will find a clear explanation of how to approach the problem and illustrative examples to guide you. Read more…