Group comparisons in structural equation models: Testing measurement invariance
When fitting almost any model, we may be interested in investigating whether parameters differ across groups such as time periods, age groups, gender, or school attended. In other words, we may wish to perform tests of moderation when the moderator variable is categorical. For regression models, this can be as simple as including group indicators in the model and interacting them with other predictors.
We naturally have hypotheses regarding differences in parameters across groups when fitting structural equation models as well. When these models involve latent variables and the corresponding observed measurements, we can test whether those measurements are invariant across groups. Evaluation of measurement invariance typically involves a series of tests for equality of measurement coefficients (factor loadings), equality of intercepts, and equality of error variances across groups.
In this post, I demonstrate how to use the sem command’s group() and ginvariant() options as well as the postestimation command estat ginvariant to easily perform tests of measurement invariance.
Measurement invariance example
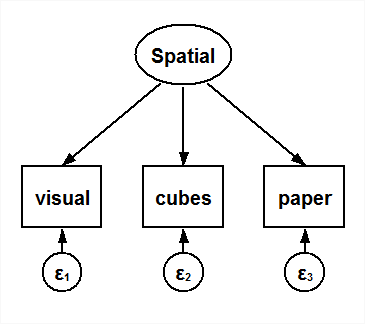
I use data from Holzinger and Swineford (1939), which records students’ scores on a number of exams designed to measure different types of abilities. The students in this dataset came from two different schools, the Pasteur school and the Grant-White school, and I want to test for differences across schools. Here I focus on three exams that were intended to measure spatial abilities. I will fit the confirmatory factor model corresponding to the following path diagram and perform a series of tests for measurement invariance. Although this example uses the sem command, I could have equivalently drawn this diagram in the Builder and selected group analysis to fit all the models discussed below.
To begin, I fit a model with all parameters estimated separately across groups. There are various ways to set the required identifying constraints that provide a scale and location for the latent variable. Here I set the mean of the Spatial latent variable to 0 and the variance to 1 in both groups.
. sem (Spatial -> visual cubes paper),
> variance(Spatial@1) mean(Spatial@0) ginvariant(none) group(school)
Endogenous variables
Measurement: visual cubes paper
Exogenous variables
Latent: Spatial
Fitting target model:
Iteration 0: log likelihood = -2603.5782
Iteration 1: log likelihood = -2603.5782
Structural equation model Number of obs = 301
Grouping variable = school Number of groups = 2
Estimation method = ml
Log likelihood = -2603.5782
( 1) [var(Spatial)]1bn.school = 1
( 2) [mean(Spatial)]1bn.school = 0
( 3) [var(Spatial)]2.school = 1
( 4) [mean(Spatial)]2.school = 0
-------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
--------------+----------------------------------------------------------------
Measurement |
visual <- |
Spatial |
Pasteur | 4.264065 .8600633 4.96 0.000 2.578372 5.949759
Grant-Wh~e | 5.49895 1.190435 4.62 0.000 3.165739 7.83216
_cons |
Pasteur | 29.64744 .5674293 52.25 0.000 28.53529 30.75958
Grant-Wh~e | 29.57931 .5721785 51.70 0.000 28.45786 30.70076
------------+----------------------------------------------------------------
cubes <- |
Spatial |
Pasteur | 2.26321 .5214501 4.34 0.000 1.241187 3.285234
Grant-Wh~e | 1.808245 .5031516 3.59 0.000 .8220861 2.794404
_cons |
Pasteur | 23.9359 .3927222 60.95 0.000 23.16618 24.70562
Grant-Wh~e | 24.8 .3678649 67.42 0.000 24.079 25.521
------------+----------------------------------------------------------------
paper <- |
Spatial |
Pasteur | 1.695466 .3429472 4.94 0.000 1.023302 2.36763
Grant-Wh~e | 1.311235 .3413206 3.84 0.000 .6422592 1.980211
_cons |
Pasteur | 14.16026 .227089 62.36 0.000 13.71517 14.60534
Grant-Wh~e | 14.30345 .2335324 61.25 0.000 13.84573 14.76116
--------------+----------------------------------------------------------------
mean(Spatial)|
[*] | 0 (constrained)
--------------+----------------------------------------------------------------
var(e.visual)|
Pasteur | 32.04601 6.912718 20.9971 48.90898
Grant-White | 17.23285 12.18676 4.309258 68.91467
var(e.cubes)|
Pasteur | 18.93787 2.710244 14.30585 25.06967
Grant-White | 16.35232 2.318816 12.38443 21.59149
var(e.paper)|
Pasteur | 5.170226 1.09911 3.408453 7.842631
Grant-White | 6.188581 .9975804 4.512114 8.487938
var(Spatial)|
[*] | 1 (constrained)
-------------------------------------------------------------------------------
Note: [*] identifies parameter estimates constrained to be equal across groups.
LR test of model vs. saturated: chi2(0) = 0.00, Prob > chi2 = .
Glancing through this output, we see that many of the parameter estimates are very similar for the two schools. The estat ginvariant command provides tests of invariance across groups.
. estat ginvariant, showpclass(mcoef) class
Tests for group invariance of parameters
------------------------------------------------------------------------------
| Wald Test Score Test
| chi2 df p>chi2 chi2 df p>chi2
-------------+----------------------------------------------------------------
Measurement |
visual <- |
Spatial | 0.707 1 0.4004 . . .
-----------+----------------------------------------------------------------
cubes <- |
Spatial | 0.394 1 0.5301 . . .
-----------+----------------------------------------------------------------
paper <- |
Spatial | 0.631 1 0.4271 . . .
------------------------------------------------------------------------------
Joint tests for each parameter class
------------------------------------------------------------------------------
| Wald Test Score Test
| chi2 df p>chi2 chi2 df p>chi2
-------------+----------------------------------------------------------------
mcoef | 1.097 3 0.7778 . . .
------------------------------------------------------------------------------
The showpclass(mcoef) and class options restricted the results to tests regarding measurement coefficients and requested a joint test for the hypothesis that all measurement coefficients are equal across groups. The first table in the output reports separate tests of equality of the measurement coefficients across groups. My focus now, however, is on the joint Wald test shown in the second table, and we fail to reject the hypothesis of equality across groups for all measurement coefficients.
I now include the ginvariant(mcoef) option in order to fit a model with the measurement coefficients constrained to be equal across groups by typing
. sem (Spatial -> visual cubes paper), variance(Spatial@1) ///
mean(Spatial@0) ginvariant(mcoef) group(school)
and then test whether the intercepts can be constrained:
. estat ginvariant, showpclass(mcons) class
Tests for group invariance of parameters
------------------------------------------------------------------------------
| Wald Test Score Test
| chi2 df p>chi2 chi2 df p>chi2
-------------+----------------------------------------------------------------
Measurement |
visual <- |
_cons | 0.007 1 0.9326 . . .
-----------+----------------------------------------------------------------
cubes <- |
_cons | 2.580 1 0.1082 . . .
-----------+----------------------------------------------------------------
paper <- |
_cons | 0.193 1 0.6605 . . .
------------------------------------------------------------------------------
Joint tests for each parameter class
------------------------------------------------------------------------------
| Wald Test Score Test
| chi2 df p>chi2 chi2 df p>chi2
-------------+----------------------------------------------------------------
mcons | 3.011 3 0.3900 . . .
------------------------------------------------------------------------------
We fail to reject the null hypothesis that all intercepts are equal across groups, so I fit the model with those equality constraints by specifying the ginvariant(mcoef mcons) option.
. sem (Spatial -> visual cubes paper), variance(Spatial@1) ///
mean(Spatial@0) ginvariant(mcoef mcons) group(school)
Then, I test the equality of the error variances.
. estat ginvariant, showpclass(merrvar) class
Tests for group invariance of parameters
------------------------------------------------------------------------------
| Wald Test Score Test
| chi2 df p>chi2 chi2 df p>chi2
-------------+----------------------------------------------------------------
var(e.visual)| 0.359 1 0.5493 . . .
var(e.cubes)| 1.413 1 0.2345 . . .
var(e.paper)| 0.014 1 0.9052 . . .
------------------------------------------------------------------------------
Joint tests for each parameter class
------------------------------------------------------------------------------
| Wald Test Score Test
| chi2 df p>chi2 chi2 df p>chi2
-------------+----------------------------------------------------------------
merrvar | 1.857 3 0.6027 . . .
------------------------------------------------------------------------------
Once again, we fail to reject the null hypothesis of invariance across groups. I now impose constraints on the coefficients, intercepts, and error variances while allowing the mean and variance of the latent variable to differ across groups. To do this, I remove the mean(Spatial@0) option and replace the variance(Spatial@1) with variance(1:Spatial@1). With this change, the mean and variance of Spatial will be set to 0 and 1, respectively, in the first group but estimated freely in the second group.
. sem (Spatial -> visual cubes paper),
> variance(1:Spatial@1) ginvariant(mcoef mcons merrvar) group(school)
Endogenous variables
Measurement: visual cubes paper
Exogenous variables
Latent: Spatial
Fitting target model:
Iteration 0: log likelihood = -5357.6935 (not concave)
Iteration 1: log likelihood = -4792.5814 (not concave)
Iteration 2: log likelihood = -4316.3827 (not concave)
Iteration 3: log likelihood = -2769.069 (not concave)
Iteration 4: log likelihood = -2662.2605
Iteration 5: log likelihood = -2645.7652
Iteration 6: log likelihood = -2629.1987
Iteration 7: log likelihood = -2622.83 (not concave)
Iteration 8: log likelihood = -2622.3555
Iteration 9: log likelihood = -2622.3227
Iteration 10: log likelihood = -2621.9007
Iteration 11: log likelihood = -2621.8931
Iteration 12: log likelihood = -2621.893
Structural equation model Number of obs = 301
Grouping variable = school Number of groups = 2
Estimation method = ml
Log likelihood = -2621.893
( 1) [cubes]1bn.school#c.Spatial - [cubes]2.school#c.Spatial = 0
( 2) [paper]1bn.school#c.Spatial - [paper]2.school#c.Spatial = 0
( 3) [var(e.visual)]1bn.school - [var(e.visual)]2.school = 0
( 4) [var(e.cubes)]1bn.school - [var(e.cubes)]2.school = 0
( 5) [var(e.paper)]1bn.school - [var(e.paper)]2.school = 0
( 6) [var(Spatial)]1bn.school = 1
( 7) [visual]1bn.school - [visual]2.school = 0
( 8) [cubes]1bn.school - [cubes]2.school = 0
( 9) [paper]1bn.school - [paper]2.school = 0
(10) [visual]2.school#c.Spatial = 1
(11) [mean(Spatial)]1bn.school = 0
-------------------------------------------------------------------------------
| OIM
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
--------------+----------------------------------------------------------------
Measurement |
visual <- |
Spatial |
Pasteur | 5.472561 1.129916 4.84 0.000 3.257966 7.687156
Grant-Wh~e | 1 (constrained)
_cons |
[*] | 29.32102 .4932735 59.44 0.000 28.35422 30.28782
------------+----------------------------------------------------------------
cubes <- |
Spatial |
[*] | .3968564 .1833049 2.17 0.030 .0375854 .7561274
_cons |
[*] | 24.26618 .2890016 83.97 0.000 23.69975 24.83262
------------+----------------------------------------------------------------
paper <- |
Spatial |
[*] | .2953686 .137265 2.15 0.031 .0263341 .5644031
_cons |
[*] | 14.16525 .1786194 79.30 0.000 13.81516 14.51533
--------------+----------------------------------------------------------------
mean(Spatial)|
Pasteur | 0 (constrained)
Grant-White | .4140109 .6928933 0.60 0.550 -.9440351 1.772057
--------------+----------------------------------------------------------------
var(e.visual)|
[*] | 19.50062 12.09195 5.784095 65.74481
var(e.cubes)|
[*] | 20.08682 1.784905 16.87617 23.90829
var(e.paper)|
[*] | 6.864085 .691005 5.634982 8.361281
var(Spatial)|
Pasteur | 1 (constrained)
Grant-White | 25.44848 15.33031 7.814351 82.87636
-------------------------------------------------------------------------------
Note: [*] identifies parameter estimates constrained to be equal across groups.
LR test of model vs. saturated: chi2(7) = 36.63, Prob > chi2 = 0.0000
The mean of 0.414 for Spatial in the Grant-White school represents the difference in means of this latent variable across schools, and we find the difference in means across schools is not significantly different from 0.
Summary
Tests of hypotheses regarding the equality of parameters across groups are easily performed using the sem command and estat ginvariant. While there are minor variations throughout structural equation modeling literature in recommendations for setting identifying constraints and for the order of tests for invariance, the tools that I have demonstrated can be adapted to accommodate any form of tests for measurement invariance. These same tools can also be used to test for parameter invariance across groups in other types of structural equation models.
Reference
Holzinger, K.~J., and F. Swineford. 1939. A study in factor analysis: The stability of a bi-factor solution. Supplementary Educational Monographs, 48. Chicago, IL: University of Chicago.