New to Stata 14 is a suite of commands to fit item response theory (IRT) models. IRT models are used to analyze the relationship between the latent trait of interest and the items intended to measure the trait. Stata’s irt commands provide easy access to some of the commonly used IRT models for binary and polytomous responses, and irtgraph commands can be used to plot item characteristic functions and information functions.

To learn more about Stata’s IRT features, I refer you to the [IRT] manual; here I want to go beyond the manual and show you a couple of examples of what you can do with a little bit of Stata code.

Example 1

To get started, I want to show you how simple IRT analysis is in Stata.

When I use the nine binary items q1–q9, all I need to type to fit a 1PL model is

irt 1pl q*

Equivalently, I can use a dash notation or explicitly spell out the variable names:

irt 1pl q1-q9
irt 1pl q1 q2 q3 q4 q5 q6 q7 q8 q9

I can also use parenthetical notation:

irt (1pl q1-q9)

Parenthetical notation is not very useful for a simple IRT model, but comes in handy when you want to fit a single IRT model to combinations of binary, ordinal, and nominal items:

irt (1pl q1-q5) (1pl q6-q9) (pcm x1-x10) ...

IRT graphs are equally simple to create in Stata; for example, to plot item characteristic curves (ICCs) for all the items in a model, I type

irtgraph icc

Yes, that’s it!

Example 2

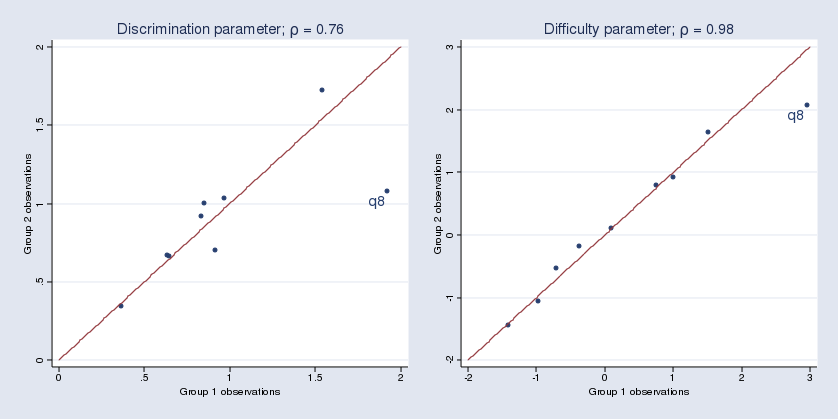
Sometimes, I want to fit the same IRT model on two different groups and see how the estimated parameters differ between the groups. The exercise can be part of investigating differential item functioning (DIF) or parameter invariance.

I split the data into two groups, fit two separate 2PL models, and create two scatterplots to see how close the parameter estimates for discrimination and difficulty are for the two groups. For simplicity, my group variable is 1 for odd-numbered observations and 0 for even-numbered observations.

We see that the estimated parameters for item q8 appear to differ between the two groups.

Here is the code used in this example.

webuse masc1, clear

gen odd = mod(_n,2)

irt 2pl q* if odd
mat b_odd = e(b)'

irt 2pl q* if !odd
mat b_even = e(b)'

svmat double b_odd, names(group1)
svmat double b_even, names(group2)
replace group11 = . in 19
replace group21 = . in 19

gen lab1 = ""
replace lab1 = "q8" in 15

gen lab2 = ""
replace lab2 = "q8" in 16

corr group11 group21 if mod(_n,2)
local c1 : display %4.2f `r(rho)'

twoway (scatter group11 group21, mlabel(lab1) mlabsize(large) mlabpos(7)) ///
        (function x, range(0 2)) if mod(_n,2), ///
        name(discr,replace) title("Discrimination parameter; {&rho} = `c1'") ///
        xtitle("Group 1 observations") ytitle("Group 2 observations") ///
        legend(off)

corr group11 group21 if !mod(_n,2)
local c2 : display %4.2f `r(rho)'

twoway (scatter group11 group21, mlabel(lab2) mlabsize(large) mlabpos(7)) ///
        (function x, range(-2 3)) if !mod(_n,2), ///
        name(diff,replace) title("Difficulty parameter; {&rho} = `c2'") ///
        xtitle("Group 1 observations") ytitle("Group 2 observations") ///
        legend(off)

graph combine discr diff, xsize(8)

Example 3

Continuing with the example above, I want to show you how to use a likelihood-ratio test to test for item parameter differences between groups.

Using item q8 as an example, I want to fit one model that constrains item q8 parameters to be the same between the two groups and fit another model that allows these parameters to vary.

The first model is easy. I can fit a 2PL model for the entire dataset, which implicitly constrains the parameters to be equal for both groups. I store the estimates under the name equal.

. webuse masc1, clear
(Data from De Boeck & Wilson (2004))

. generate odd = mod(_n,2)
. quietly irt 2pl q*
. estimates store equal

To estimate the second model, I need the following:

. irt (2pl q1-q7 q9) (2pl q8 if odd) (2pl q8 if !odd)

Unfortunately, this is illegal syntax. I can, however, split the item into two new variables where each variable is restricted to the required subsample:

. generate q8_1 = q8 if odd
(400 missing values generated)

. generate q8_2 = q8 if !odd
(400 missing values generated)

I estimate the second IRT model, this time with items q8_1 and q8_2 taking place of the original q8:

. quietly irt 2pl q1-q7 q8_1 q8_2 q9
. estat report q8_1 q8_2

Two-parameter logistic model                    Number of obs     =        800
Log likelihood = -4116.2064
------------------------------------------------------------------------------
             |      Coef.   Std. Err.      z    P>|z|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
q8_1         |
     Discrim |   1.095867   .2647727     4.14   0.000     .5769218    1.614812
        Diff |  -1.886126   .3491548    -5.40   0.000    -2.570457   -1.201795
-------------+----------------------------------------------------------------
q8_2         |
     Discrim |    1.93005   .4731355     4.08   0.000     1.002721    2.857378
        Diff |  -1.544908   .2011934    -7.68   0.000     -1.93924   -1.150577
------------------------------------------------------------------------------

Now, I can perform the likelihood-ratio test:

. lrtest equal ., force

Likelihood-ratio test                                 LR chi2(2)  =      4.53
(Assumption: equal nested in .)                       Prob > chi2 =    0.1040

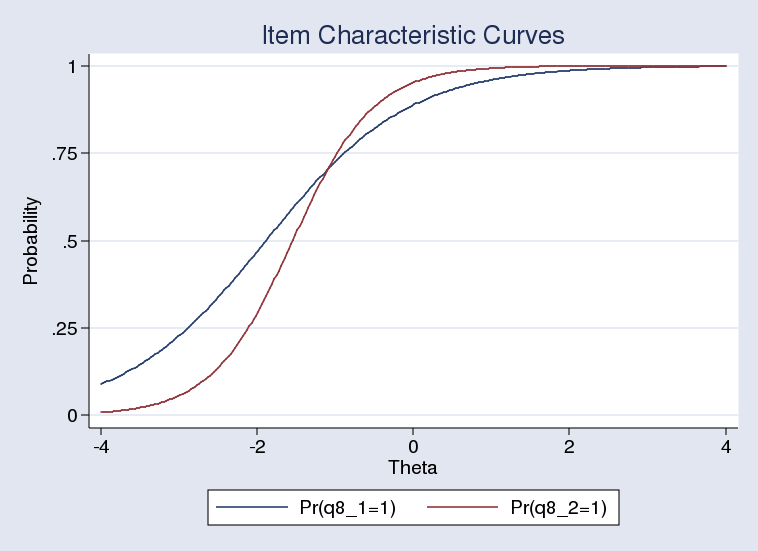
The test suggests the first model is preferable even though the two ICCs clearly differ:

. irtgraph icc q8_1 q8_2, ylabel(0(.25)1)

Summary

IRT models are used to analyze the relationship between the latent trait of interest and the items intended to measure the trait. Stata’s irt commands provide easy access to some of the commonly used IRT models, and irtgraph commands implement the most commonly used IRT plots. With just a few extra steps, you can easily create customized graphs, such as the ones demonstrated above, which incorporate information from separate IRT models.