Measures of effect size in Stata 13
Today I want to talk about effect sizes such as Cohen’s d, Hedges’s g, Glass’s Δ, η2, and ω2. Effects sizes concern rescaling parameter estimates to make them easier to interpret, especially in terms of practical significance.
Many researchers in psychology and education advocate reporting of effect sizes, professional organizations such as the American Psychological Association (APA) and the American Educational Research Association (AERA) strongly recommend their reporting, and professional journals such as the Journal of Experimental Psychology: Applied and Educational and Psychological Measurement require that they be reported.
Anyway, today I want to show you
- What effect sizes are.
- How to calculate effect sizes and their confidence intervals in Stata.
- How to calculate bootstrap confidence intervals for those effect sizes.
- How to use Stata’s effect-size calculator.
1. What are effect sizes?
The importance of research results is often assessed by statistical significance, usually that the p-value is less than 0.05. P-values and statistical significance, however, don’t tell us anything about practical significance.
What if I told you that I had developed a new weight-loss pill and that the difference between the average weight loss for people who took the pill and the those who took a placebo was statistically significant? Would you buy my new pill? If you were overweight, you might reply, “Of course! I’ll take two bottles and a large order of french fries to go!”. Now let me add that the average difference in weight loss was only one pound over the year. Still interested? My results may be statistically significant but they are not practically significant.
Or what if I told you that the difference in weight loss was not statistically significant — the p-value was “only” 0.06 — but the average difference over the year was 20 pounds? You might very well be interested in that pill.
The size of the effect tells us about the practical significance. P-values do not assess practical significance.
All of which is to say, one should report parameter estimates along with statistical significance.
In my examples above, you knew that 1 pound over the year is small and 20 pounds is large because you are familiar with human weights.
In another context, 1 pound might be large, and in yet another, 20 pounds small.
Formal measures of effects sizes are thus usually presented in unit-free but easy-to-interpret form, such as standardized differences and proportions of variability explained.
The “d” family
Effect sizes that measure the scaled difference between means belong to the “d” family. The generic formula is
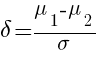
The estimators differ in terms of how sigma is calculated.
Cohen’s d, for instance, uses the pooled sample standard deviation.
Hedges’s g incorporates an adjustment which removes the bias of Cohen’s d.
Glass’s Δ was originally developed in the context of experiments and uses the “control group” standard deviation in the denominator. It has subsequently been generalized to nonexperimental studies. Because there is no control group in observational studies, Kline (2013) recommends reporting Glass’s Δ using the standard deviation for each group. Glass’s Delta_1 uses one group’s standard deviation and Delta_2 uses the other group’s.
Although I have given definitions to Cohen’s d, Hedges’s g, and Glass’s Δ, different authors swap the definitions around! As a result, many authors refer to all of the above as just Delta.
Be careful when using software to know which Delta you are getting. I have used Stata terminology, of course.
Anyway, the use of a standardized scale allows us to assess of practical significance. Delta = 1.5 indicates that the mean of one group is 1.5 standard deviations higher than that of the other. A difference of 1.5 standard deviations is obviously large, and a difference of 0.1 standard deviations is obviously small.
The “r” family
The r family quantifies the ratio of the variance attributable to an effect to the total variance and is often interpreted as the “proportion of variance explained”. The generic estimator is known as eta-squared,
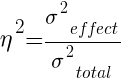
η2 is equivalent to the R-squared statistic from linear regression.
ω2 is a less biased variation of η2 that is equivalent to the adjusted R-squared.
Both of these measures concern the entire model.
Partial η2 and partial ω2 are like partial R-squareds and concern individual terms in the model. A term might be a variable or a variable and its interaction with another variable.
Both the d and r families allow us to make an apples-to-apples comparison of variables measured on different scales. For example, an intervention could affect both systolic blood pressure and total cholesterol. Comparing the relative effect of the intervention on the two outcomes would be difficult on their original scales.
How does one compare mm/Hg and mg/dL? It is straightforward in terms of Cohen’s d or ω2 because then we are comparing standard deviation changes or proportion of variance explained.
2. How to calculate effect sizes and their confidence intervals in Stata
Consider a study where 30 school children are randomly assigned to classrooms that incorporated web-based instruction (treatment) or standard classroom environments (control). At the end of the school year, the children were given tests to measure reading and mathematics skills. The reading test is scored on a 0-15 point scale and, the mathematics test, on a 0-100 point scale.
Let’s download a dataset for our fictitious example from the Stata website by typing:
. use http://www.stata.com/videos13/data/webclass.dta
Contains data from http://www.stata.com/videos13/data/webclass.dta
obs: 30 Fictitious web-based learning
experiment data
vars: 5 5 Sep 2013 11:28
size: 330 (_dta has notes)
-------------------------------------------------------------------------------
storage display value
variable name type format label variable label
-------------------------------------------------------------------------------
id byte %9.0g ID Number
treated byte %9.0g treated Treatment Group
agegroup byte %9.0g agegroup Age Group
reading float %9.0g Reading Score
math float %9.0g Math Score
-------------------------------------------------------------------------------
. notes
_dta:
1. Variable treated records 0=control, 1=treated.
2. Variable agegroup records 1=7 years old, 2=8 years old, 3=9 years old.
We can compute a t-statistic to test the null hypothesis that the average math scores are the same in the treatment and control groups.
. ttest math, by(treated)
Two-sample t test with equal variances
------------------------------------------------------------------------------
Group | Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
---------+--------------------------------------------------------------------
Control | 15 69.98866 3.232864 12.52083 63.05485 76.92246
Treated | 15 79.54943 1.812756 7.020772 75.66146 83.4374
---------+--------------------------------------------------------------------
combined | 30 74.76904 2.025821 11.09588 70.62577 78.91231
---------+--------------------------------------------------------------------
diff | -9.560774 3.706412 -17.15301 -1.968533
------------------------------------------------------------------------------
diff = mean(Control) - mean(Treated) t = -2.5795
Ho: diff = 0 degrees of freedom = 28
Ha: diff < 0 Ha: diff != 0 Ha: diff > 0
Pr(T < t) = 0.0077 Pr(|T| > |t|) = 0.0154 Pr(T > t) = 0.9923
The treated students have a larger mean, yet the difference of -9.56 is reported as negative because -ttest- calculated Control minus Treated. So just remember, negative differences mean Treated > Control in this case.
The t-statistic equals -2.58 and its two-sided p-value of 0.0154 indicates that the difference between the math scores in the two groups is statistically significant.
Next, let’s calculate effect sizes from the d family:
. esize twosample math, by(treated) cohensd hedgesg glassdelta
Effect size based on mean comparison
Obs per group:
Control = 15
Treated = 15
---------------------------------------------------------
Effect Size | Estimate [95% Conf. Interval]
--------------------+------------------------------------
Cohen's d | -.9419085 -1.691029 -.1777553
Hedges's g | -.916413 -1.645256 -.1729438
Glass's Delta 1 | -.7635896 -1.52044 .0167094
Glass's Delta 2 | -1.361784 -2.218342 -.4727376
---------------------------------------------------------
Cohen’s d and Hedges’s g both indicate that the average reading scores differ by approximately -0.93 standard deviations with 95% confidence intervals of (-1.69, -0.18) and (-1.65, -0.17) respectively.
Since this is an experiment, we are interested in Glass’s Delta 1 because it is calculated using the control group standard deviation. Average reading scores differ by -0.76 and the confidence interval is (-1.52, 0.02).
The confidence intervals for Cohen’s d and Hedges’s g do not include the null value of zero but the confidence interval for Glass’s Delta 1 does. Thus we cannot completely rule out the possibility that the treatment had no effect on math scores.
Next we could incorporate the age group of the children into our analysis by using a two-way ANOVA to test the null hypothesis that the mean math scores are equal for all groups.
. anova math treated##agegroup
Number of obs = 30 R-squared = 0.2671
Root MSE = 10.4418 Adj R-squared = 0.1144
Source | Partial SS df MS F Prob > F
-----------------+----------------------------------------------------
Model | 953.697551 5 190.73951 1.75 0.1617
|
treated | 685.562956 1 685.562956 6.29 0.0193
agegroup | 47.7059268 2 23.8529634 0.22 0.8051
treated#agegroup | 220.428668 2 110.214334 1.01 0.3789
|
Residual | 2616.73825 24 109.030761
-----------------+----------------------------------------------------
Total | 3570.4358 29 123.118476
The F-statistic for the entire model is not statistically significant (F=1.75, ndf=5, ddf=24, p=0.1617) but the F-statistic for the main effect of treatment is statistically significant (F=6.29, ndf=1, ddf=24, p=0.0193).
We can compute the η2 and partial η2 estimates for this model using the estat esize command immediately after our anova command (note that estat esize works after the regress command too).
. estat esize
Effect sizes for linear models
---------------------------------------------------------------------
Source | Eta-Squared df [95% Conf. Interval]
----------------------+----------------------------------------------
Model | .2671096 5 0 .4067062
|
treated | .2076016 1 .0039512 .4451877
agegroup | .0179046 2 0 .1458161
treated#agegroup | .0776932 2 0 .271507
---------------------------------------------------------------------
The overall η2 indicates that our model accounts for approximately 26.7% of the variablity in math scores though the 95% confidence interval includes the null value of zero (0.00%, 40.7%). The partial η2 for treatment is 0.21 (21% of the variability explained) and its 95% confidence interval excludes zero (0.3%, 20%).
We could calculate the alternative r-family member ω2 rather than η2 by typing
. estat esize, omega
Effect sizes for linear models
---------------------------------------------------------------------
Source | Omega-Squared df [95% Conf. Interval]
----------------------+----------------------------------------------
Model | .1144241 5 0 .2831033
|
treated | .174585 1 0 .4220705
agegroup | 0 2 0 .0746342
treated#agegroup | .0008343 2 0 .2107992
---------------------------------------------------------------------
The overall ω2 indicates that our model accounts for approximately 11.4% of the variability in math scores and treatment accounts for 17.5%. This perplexing result stems from the way that ω2 and partial ω2 are calculated. See Pierce, Block, & Aguinis (2004) for a thorough explanation.
Except for the η2 for treatment, the confidence intervals include 0 so we cannot rule out the possibility that there is no effect. Whether results are practically significant is generically a matter context and opinion. In some situations, accounting for 5% of the variability in an outcome could be very important and in other situations accounting for 30% may not be.
We could repeat the same analyses for the reading scores using the following commands:
. ttest reading, by(treated) . esize twosample reading, by(treated) cohensd hedgesg glassdelta . anova reading treated##agegroup . estat esize . estat esize, omega
None of the t- or F-statistics for reading scores were statistically significant at the 0.05 level.
Even though the reading and math scores were measured on two different scales, we can directly compare the relative effect of the treatment using effect sizes:
Effect Size | Reading Score Math Score
------------------------------------------------------------
Cohen's d | -0.23 (-0.95 - 0.49) -0.94 (-1.69 - -0.18)
Hedges's g | -0.22 (-0.92 - 0.48) -0.92 (-1.65 - -0.17)
Glass's Delta | -0.21 (-0.93 - 0.51) -0.76 (-1.52 - 0.02)
Eta-squared | 0.02 ( 0.00 - 0.20) 0.21 ( 0.00 - 0.44)
Omega-squared | 0.00 ( 0.00 - 0.17) 0.17 ( 0.00 - 0.42)
The results show that the average reading scores in the treated and control groups differ by approximately 0.22 standard deviations while the average math scores differ by approximately 0.92 standard deviations. Similarly, treatment status accounted for almost none of the variability in reading scores while it accounted for roughly 17% of the variability in math scores. The intervention clearly had a larger effect on math scores than reading scores. We also know that we cannot completely rule out an effect size of zero (no effect) for both reading and math scores because several confidence intervals included zero. Whether or not the effects are practically significant is a matter of interpretation but the effect sizes provide a standardized metric for evaluation.
3. How to calculate bootstrap confidence intervals
Simulation studies have shown that bootstrap confidence intervals for the d family may be preferable to confidence intervals based on the noncentral t distribution when the variable of interest does not have a normal distribution (Kelley 2005; Algina, Keselman, and Penfield 2006). We can calculate bootstrap confidence intervals for Cohen’s d and Hedges’s g using Stata’s bootstrap prefix:
. bootstrap r(d) r(g), reps(500) nowarn: esize twosample reading, by(treated)
(running esize on estimation sample)
Bootstrap replications (500)
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5
.................................................. 50
.................................................. 100
.................................................. 150
.................................................. 200
.................................................. 250
.................................................. 300
.................................................. 350
.................................................. 400
.................................................. 450
.................................................. 500
Bootstrap results Number of obs = 30
Replications = 500
command: esize twosample reading, by(treated)
_bs_1: r(d)
_bs_2: r(g)
------------------------------------------------------------------------------
| Observed Bootstrap Normal-based
| Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_bs_1 | -.228966 .3905644 -0.59 0.558 -.9944582 .5365262
_bs_2 | -.2227684 .3799927 -0.59 0.558 -.9675403 .5220036
------------------------------------------------------------------------------
The bootstrap estimate of the 95% confidence interval for Cohen’s d is -0.99 to 0.54 which is slightly wider than the earlier estimate based on the non-central t distribution (see [R] esize for details). The bootstrap estimate is slightly wider for Hedges’s g as well.
4. How to use Stata’s effect-size calculator
You can use Stata’s effect size calculators to estimate them using summary statistics. If we know that the mean, standard deviation and sample size for one group is 70, 12.5 and 15 respectively and 80, 7 and 15 for another group, we can use esizei to estimate effect sizes from the d family:
. esizei 15 70 12.5 15 80 7, cohensd hedgesg glassdelta
Effect size based on mean comparison
Obs per group:
Group 1 = 15
Group 2 = 15
---------------------------------------------------------
Effect Size | Estimate [95% Conf. Interval]
--------------------+------------------------------------
Cohen's d | -.9871279 -1.739873 -.2187839
Hedges's g | -.9604084 -1.692779 -.2128619
Glass's Delta 1 | -.8 -1.561417 -.0143276
Glass's Delta 2 | -1.428571 -2.299112 -.5250285
---------------------------------------------------------
We can estimate effect sizes from the r family using esizei with slightly different syntax. For example, if we know the numerator and denominator degrees of freedom along with the F statistic, we can calculate η2 and ω2 using the following command:
. esizei 1 28 6.65
Effect sizes for linear models
---------------------------------------------------------
Effect Size | Estimate [95% Conf. Interval]
--------------------+------------------------------------
Eta-Squared | .1919192 .0065357 .4167874
Omega-Squared | .1630592 0 .3959584
---------------------------------------------------------
Video demonstration
Stata has dialog boxes that can assist you in calculating effect sizes. If you would like a brief introduction using the GUI, you can watch a demonstration on Stata’s YouTube Channel:
Final thoughts and further reading
Most older papers and many current papers do not report effect sizes. Nowadays, the general consensus among behavioral scientists, their professional organizations, and their journals is that effect sizes should always be reported in addition to tests of statistical significance. Stata 13 now makes it easy to compute most popular effects sizes.
Some methodologists believe that effect sizes with confidence intervals should always be reported and that statistical hypothesis tests should be abandoned altogether; see Cumming (2012) and Kline (2013). While this may sound like a radical notion, other fields such as epidemiology have been moving in this direction since the 1990s. Cumming and Kline offer compelling arguments for this paradigm shift as well as excellent introductions to effect sizes.
American Psychological Association (2009). Publication Manual of the American Psychological Association, 6th Ed. Washington, DC: American Psychological Association.
Algina, J., H. J. Keselman, and R. D. Penfield. (2006). Confidence interval coverage for Cohen’s effect size statistic. Educational and Psychological Measurement, 66(6): 945–960.
Cumming, G. (2012). Understanding the New Statistics: Effect Sizes, Confidence Intervals, and Meta-Analysis. New York: Taylor & Francis.
Kelley, K. (2005). The effects of nonnormal distributions on confidence intervals around the standardized mean difference: Bootstrap and parametric confidence intervals. Educational and Psychological Measurement 65: 51–69.
Kirk, R. (1996). Practical significance: A concept whose time has come. Educational and Psychological Measurement, 56, 746-759.
Kline, R. B. (2013). Beyond Significance Testing: Statistics Reform in the Behavioral Sciences. 2nd ed. Washington, DC: American Psychological Association.
Pierce, C.A., Block, R. A., and Aguinis, H. (2004). Cautionary note on reporting eta-squared values from multifactor ANOVA designs. Educational and Psychological Measurement, 64(6) 916-924
Thompson, B. (1996) AERA Editorial Policies regarding Statistical Significance Testing: Three Suggested Reforms. Educational Researcher, 25(2) 26-30
Wilkinson, L., & APA Task Force on Statistical Inference. (1999). Statistical methods in psychology journals: Guidelines and explanations. American Psychologist, 54, 594-604