Comparing transmissibility of Omicron lineages
Monitoring lineages of the Omicron variant of the SARS-CoV-2 virus continues to be an important health consideration. The World Health Organization identifies BA.1, BA.1.1, and the most recent BA.2 as the most common sublineages. A recent study from Japan, Yamasoba et al. (2022), compares, among other characteristics, the transmissibility of these three Omicron lineages with the latest Delta variant. It identifies BA.2 to have the highest transmissibility of the four. Preprint of the study is available at bioarxiv.org. One interesting aspect of the study is the application of Bayesian multilevel models for representing lineage growth dynamics. In this post, I demonstrate how to use Stata’s bayesmh and bayesstats summary commands to perform similar analysis.
The datasets are available at github.com. The data were compiled from the GISAID database, https://www.gisaid.org/hcov19-variants/, on February 1, 2022.
Observations on the number of cases for each lineage are collected for 11 countries in a period of 117 days, from October 1, 2021, to January 25, 2022.
. use omicron_ba2
. summarize
Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
day | 1,185 58.18312 33.1129 1 117
yba1 | 1,185 377.2878 1301.07 0 10251
yba11 | 1,185 168.5561 685.6369 0 7378
yba2 | 1,185 23.60759 128.7147 0 1481
ydelta | 1,185 1224.78 2513.555 0 12549
-------------+---------------------------------------------------------
country | 1,185 6.03038 3.245177 1 11
The variables yba1, yba11, yba2, and ydelta correspond, respectively, to the number of cases of BA.1, BA.1.1, and BA.2 lineages and the Delta variant. The variables day and country identify the day and country, respectively. The following table shows the country codes and the number of observed days for each country.
| Id | Country | Days |
| 1 | Austria | 105 |
| 2 | Denmark | 116 |
| 3 | Germany | 116 |
| 4 | India | 117 |
| 5 | Israel | 117 |
| 6 | Philippines | 43 |
| 7 | Singapore | 115 |
| 8 | South Africa | 110 |
| 9 | Swiden | 112 |
| 10 | United Kingdom | 117 |
| 11 | USA | 117 |
For some countries, the data are incomplete. In particular, for the Philippines, data are available for only 43 days, which, as we will see later, affects the analysis.
Bayesian multilevel multinomial model
In each of the 11 countries, the viral lineages are recorded as the number of cases on the observed days. To formally specify the model, let us denote variables yba1, yba11, yba2, and ydelta, respectively, as \(y_{1ct}\), \(y_{2ct}\), \(y_{3ct}\), and \(y_{4ct}\), where \(c\) is the country code and \(t\) is the observation time. \(y_{lct}\) is assumed to follow a multinomial distribution with total number of cases \(n_{ct}\). The probability of an occurrence of a lineage, \(\theta_{lct}\), for lineage \(l\), country \(c\), and time \(t\) is given by the 4-dimensional logistic function (softmax) applied to linear functions \(a_{lc} + b_{lc}\times t\), where \(a_{lc}\) and, \(b_{lc}\) are random-effect parameters.
More formally, for lineages \(l=1,\dots,4\) and countries \(c=1,\dots,11\), we have
$$
y_{lct} \sim {\rm Multinomial}(n_{ct}, \theta_{lct})\\
\theta_{lct} = \frac{{\rm exp}(\mu_{lct})}{\sum_{k=1}^4 {\rm exp}(\mu_{kct})}\hspace{.5cm}\\
\mu_{lct} = a_{lc} + b_{lc} \times t \hspace{1.5cm}
$$
The probability of observing counts \(n_1\) through \(n_4\), where \(n_1+n_2+n_3+n_4=n_{ct}\), is
$$
P(y_{1ct}=n_1, y_{2ct}=n_2, y_{3ct}=n_3, y_{4ct}=n_4) =
\frac{n_{ct}!}{n_1!n_2!n_3!n_4!}
\theta_{1ct}^{n_1}\theta_{2ct}^{n_2}\theta_{3ct}^{n_3}\theta_{4ct}^{n_4}
$$
For identifiability, I set the random parameters for the BA.1 lineage, \(a_{1c}\) and \(b_{1c}\), to 0. In this case, we have
$$
\theta_{1ct} = \frac{1}{1+\sum_{k=2}^4 {\rm exp}(\mu_{kct})}\\
\theta_{2ct} = \frac{{\rm exp}(\mu_{2ct})}{1+\sum_{k=2}^4 {\rm exp}(\mu_{kct})}\\
\theta_{3ct} = \frac{{\rm exp}(\mu_{3ct})}{1+\sum_{k=2}^4 {\rm exp}(\mu_{kct})}\\
\theta_{4ct} = \frac{{\rm exp}(\mu_{4ct})}{1+\sum_{k=2}^4 {\rm exp}(\mu_{kct})}
$$
and the \(lct\)-observation of the log likelihood is
$$
{\rm const} + y_{2ct}\times\mu_{2ct} + y_{3ct}\times\mu_{3ct} + y_{4ct}\times\mu_{4ct} \\
\hspace{1cm}- n_{ct}\times\{1+{\rm exp}(\mu_{2ct})+ {\rm exp}(\mu_{3ct})+ {\rm exp}(\mu_{4ct})\}
$$
For the purpose of sampling the posterior model, we can ignore the constant terms.
The authors propose Student’s \(t\)-distributions with 6 degrees of freedom for the random slope parameters \(b_{lc}\) to reduce the effects of outliers,
$$
b_{lc} \sim t_6(\beta_l, \sigma_l^2)
$$
and flat priors for the random intercepts \(a_{lc}\) and hyperparameters \(\beta_l\) and \(\sigma_l^2\). Instead, to have a proper prior model, I apply weakly informative priors: \(N(0, 100)\) for random intercepts \(a_{lc}\)s and random slopes \(\beta_{l}\)s and \({\rm InvGamma}(0.1,0.1)\) for the variance parameters \(\sigma_l^2\)s.
To compute the log likelihood, I define a new variable, ytotal, for the total number cases \(n_{ct}\).
. gen double ytotal = yba1+yba11+yba2+ydelta
Because we don’t have a built-in distribution in bayesmh for this likelihood model, I use the llf() option to specify it according to the above formula. The llf() option requires a univariate model specification, so I use ytotal as a dependent variable representing the vector of counts \((y_{1ct},y_{2ct},y_{3ct},y_{4ct})\).
The linear combinations \(\mu_{2ct}\), \(\mu_{3ct}\), and \(\mu_{4ct}\) are specified using the define() option. The latter include random intercepts A2[country], A3[country], and A4[country] and random slopes B2[country], B3[country], and B4[country]. The random slopes describe the transmissibility of the lineages in comparison with BA.1.
To improve the sampling, I block some of the parameters and provide initial values within the domain of the posterior.
. bayesmh ytotal, noconstant likelihood(llf(
> yba11*{mu2:}+yba2*{mu3:}+ydelta*{mu4:} -
> ytotal*ln(1+exp({mu2:})+exp({mu3:})+exp({mu4:}))))
> define(mu2: A2[country] B2[country]#c.day, noconstant)
> define(mu3: A3[country] B3[country]#c.day, noconstant)
> define(mu4: A4[country] B4[country]#c.day, noconstant)
> prior({A2}, normal(0, 100))
> prior({A3}, normal(0, 100))
> prior({A4}, normal(0, 100))
> prior({B2}, t({beta2}, {sigma2}, 6))
> prior({B3}, t({beta3}, {sigma3}, 6))
> prior({B4}, t({beta4}, {sigma4}, 6))
> prior({sigma2 sigma3 sigma4}, igamma(0.1, 0.1) split)
> prior({beta2 beta3 beta4}, normal(0, 100) split)
> block({beta2 sigma2})
> block({beta3 sigma3}) block({beta4 sigma4})
> init({beta2 beta3 beta4} rnormal(1, 1)
> {sigma2 sigma3 sigma4} 1) rseed(17)
Burn-in 2500 aaaaaaaaa1000aaaaaaaaa2000aaaaa done
Simulation 10000 .........1000.........2000.........3000.........4000.........
> 5000.........6000.........7000.........8000.........9000.........10000 done
Model summary
------------------------------------------------------------------------------
Likelihood:
ytotal ~ logdensity()
Hyperpriors:
{A2[country] A3[country] A4[country]} ~ normal(0,100)
{B2[country]} ~ t({beta2},{sigma2},6)
{B3[country]} ~ t({beta3},{sigma3},6)
{B4[country]} ~ t({beta4},{sigma4},6)
{sigma2 sigma3 sigma4} ~ igamma(0.1,0.1)
{beta2 beta3 beta4} ~ normal(0,100)
Expression:
expr4 : yba11*xb_mu2+yba2*xb_mu3+ydelta*xb_mu4-ytotal*ln(1+exp(xb_mu2)
+exp(xb_mu3)+exp(xb_mu4))
------------------------------------------------------------------------------
Bayesian regression MCMC iterations = 12,500
Random-walk Metropolis–Hastings sampling Burn-in = 2,500
MCMC sample size = 10,000
Number of obs = 1,185
Acceptance rate = .2528
Efficiency: min = .02015
avg = .06866
Log marginal-likelihood max = .09676
------------------------------------------------------------------------------
| Equal-tailed
| Mean Std. dev. MCSE Median [95% cred. interval]
-------------+----------------------------------------------------------------
beta2 | .0271004 .04504 .001448 .026472 -.0587521 .1217648
sigma2 | .0245979 .0132208 .000554 .0207922 .010104 .0613864
beta3 | .1527336 .0530795 .001722 .1533625 .0424005 .2561617
sigma3 | .0304257 .0174173 .000794 .0260487 .0112527 .0827476
beta4 | -.1673996 .0474555 .001539 -.1678558 -.2638208 -.0749281
sigma4 | .0264834 .0164447 .001159 .0227708 .010781 .0628222
------------------------------------------------------------------------------
There are no obvious convergence issues with the model, and the 7% average sampling efficiency for the hyperparameters is good.
The positive estimate for beta2 and beta3 suggests that BA.1.1 and BA.2 lineages are both more transmittable than BA.1. On the other hand, the posterior mean estimate for beta4 is negative, \(-0.17\), implying less transmittability of Delta in comparison with the original Omicron BA.1.
Relative effective reproduction by country
The authors of the study calculate the relative effective reproduction number according to the formula
$$
r_{lc} = {\rm exp}(\gamma\beta_{lc})
$$
and the average relative effective reproduction number across countries according to
$$
r_{l} = {\rm exp}(\gamma\beta_{l})
$$
where \(\gamma\) is the viral generation time, 2.1 days; see Estimating Generation Time of Omicron.
We estimate the reproduction numbers \(r_l\) using the bayesstats summary command. Because we assumed BA.1 lineage to be the baseline, the reproduction numbers are relative to BA.1.
. bayesstats summary (rba11:exp(2.1*{beta2}))
> (rba2:exp(2.1*{beta3})) (rdelta:exp(2.1*{beta4}))
Posterior summary statistics MCMC sample size = 10,000
rba11 : exp(2.1* { beta2 } )
rba2 : exp(2.1* { beta3 } )
rdelta : exp(2.1* { beta4 } )
------------------------------------------------------------------------------
| Equal-tailed
| Mean Std. dev. MCSE Median [95% cred. interval]
-------------+----------------------------------------------------------------
rba11 | 1.063311 .1011051 .003258 1.057165 .8839283 1.291373
rba2 | 1.38671 .1545093 .00502 1.379969 1.093126 1.712475
rdelta | .7070996 .0705203 .002292 .7029306 .574633 .8544061
------------------------------------------------------------------------------
Based on posterior mean estimates, the reproduction of BA.1.1 is about 6% higher, BA.2 is about 39% higher, and Delta is about 30% lower than that of BA.1. These results agree with the findings in the paper that BA.2 has 1.4-fold higher effective reproduction than that of BA.1.
Below, I show caterpillar plots for the relative effective reproduction numbers by country. Plotted are the posterior mean values along with 95% credible intervals.
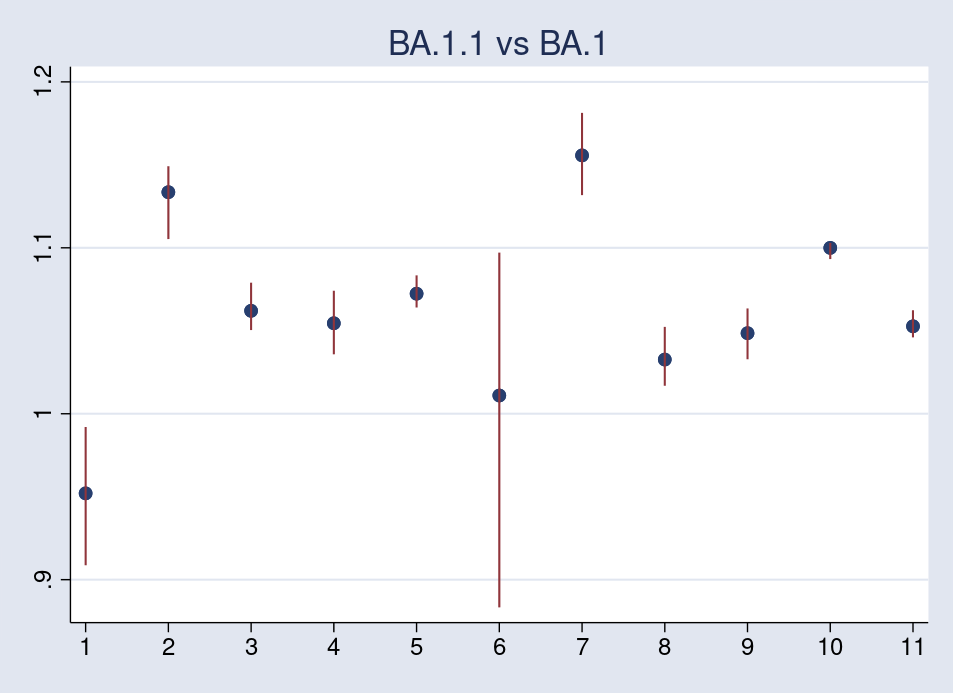
The first plot compares BA.1.1 with BA.1.
. gen id = mod(_n-1, 11)+1
. quietly bayesstats summary (exp(2.1*{B2[country]}))
. mat bsum = r(summary)
. mat bsum = (bsum[1..11,1], bsum[1..11,5], bsum[1..11,6])
. svmat bsum
. twoway scatter bsum1 id || rspike bsum3 bsum2 id, legend(off)
> xla(1 2 3 4 5 6 7 8 9 10 11, valuelabel) xsc(r(1 11))
> xtitle("") title("BA.1.1 vs BA.1")
. drop bsum*
All the values are greater than 1 except for country 1, Austria. Also apparent is the wide credible interval for country 6, Philippines, due, probably, to the much fewer observation days available, only 43, in comparison with the other countries, 110 or more.
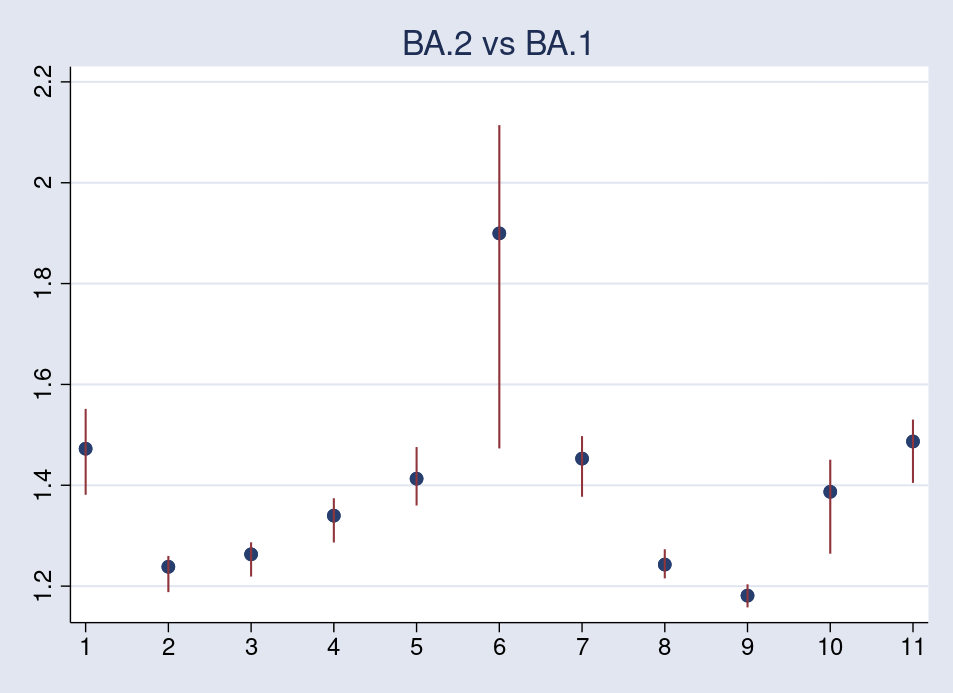
The second plot compares BA.2 with BA.1.
. quietly bayesstats summary (exp(2.1*{B3[country]}))
. mat bsum = r(summary)
. mat bsum = (bsum[1..11,1], bsum[1..11,5], bsum[1..11,6])
. svmat bsum
. twoway scatter bsum1 id || rspike bsum3 bsum2 id, legend(off)
> xla(1 2 3 4 5 6 7 8 9 10 11, valuelabel) xsc(r(1 11))
> xtitle("") title("BA.2 vs BA.1")
. drop bsum*
Again, the reproduction number for the Philippines has higher variability and tends to shift the average across-country reproduction upward.
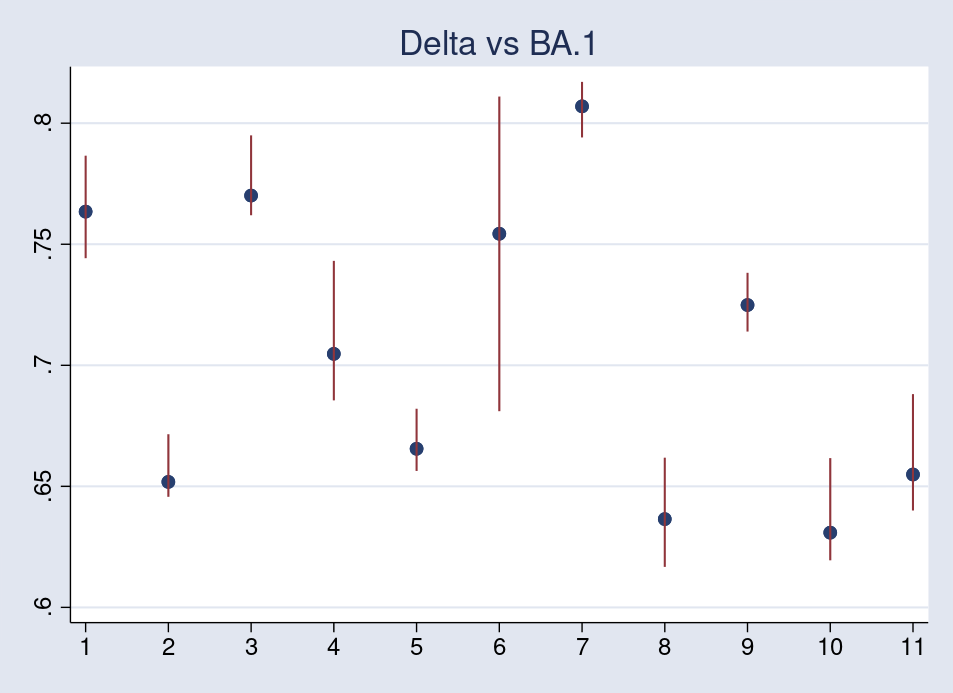
The third plot compares Delta with BA.1.
. quietly bayesstats summary (exp(2.1*{B4[country]}))
. mat bsum = r(summary)
. mat bsum = (bsum[1..11,1], bsum[1..11,5], bsum[1..11,6])
. svmat bsum
. twoway scatter bsum1 id || rspike bsum3 bsum2 id, legend(off)
> xla(1 2 3 4 5 6 7 8 9 10 11, valuelabel) xsc(r(1 11))
> xtitle("") title("Delta vs BA.1")
. drop bsum*
As we might anticipate, all reproduction numbers are less than 1, and the reproduction number for the Philippines has higher variability than the others.
Sensitivity analysis
The authors of the study use Student’s \(t\)-prior with 6 degrees of freedom for the random slopes \(b_{lc}\). It is interesting to check whether changing the prior affects the results in any substantive way.
Below, I fit models using \(t\)-priors with 2 and 12 degrees of freedom for \(b_{lc}\).
. quietly bayesmh ytotal, noconstant likelihood(llf(
> yba11*{mu2:}+yba2*{mu3:}+ydelta*{mu4:} -
> ytotal*ln(1+exp({mu2:})+exp({mu3:})+exp({mu4:}))))
> define(mu2: A2[country] B2[country]#c.day, noconstant)
> define(mu3: A3[country] B3[country]#c.day, noconstant)
> define(mu4: A4[country] B4[country]#c.day, noconstant)
> prior({A2}, normal(0, 100))
> prior({A3}, normal(0, 100))
> prior({A4}, normal(0, 100))
> prior({B2}, t({beta2}, {sigma2}, 2))
> prior({B3}, t({beta3}, {sigma3}, 2))
> prior({B4}, t({beta4}, {sigma4}, 2))
> prior({sigma2}{sigma3}{sigma4}, igamma(0.1, 0.1) split)
> prior({beta2}{beta3}{beta4}, normal(0, 100) split)
> block({beta2}{sigma2})
> block({beta3}{sigma3}) block({beta4}{sigma4})
> init({beta2}{beta3}{beta4} rnormal(1, 1)
> {sigma2}{sigma3}{sigma4} 1)
> burnin(5000) rseed(17)
. bayesstats summary (r2:exp(2.1*{beta2}))
> (r3:exp(2.1*{beta3})) (r4:exp(2.1*{beta4}))
Posterior summary statistics MCMC sample size = 10,000
r2 : exp(2.1* { beta2 } )
r3 : exp(2.1* { beta3 } )
r4 : exp(2.1* { beta4 } )
------------------------------------------------------------------------------
| Equal-tailed
| Mean Std. dev. MCSE Median [95% cred. interval]
-------------+----------------------------------------------------------------
r2 | 1.067439 .0938958 .003041 1.060892 .8874384 1.262244
r3 | 1.394932 .1392574 .006867 1.381163 1.163633 1.702113
r4 | .700393 .0654377 .001962 .6977034 .5754148 .8349086
------------------------------------------------------------------------------
. quietly bayesmh ytotal, noconstant likelihood(llf(
> yba11*{mu2:}+yba2*{mu3:}+ydelta*{mu4:} -
> ytotal*ln(1+exp({mu2:})+exp({mu3:})+exp({mu4:}))))
> define(mu2: A2[country] B2[country]#c.day, noconstant)
> define(mu3: A3[country] B3[country]#c.day, noconstant)
> define(mu4: A4[country] B4[country]#c.day, noconstant)
> prior({A2}, normal(0, 100))
> prior({A3}, normal(0, 100))
> prior({A4}, normal(0, 100))
> prior({B2}, t({beta2}, {sigma2}, 12))
> prior({B3}, t({beta3}, {sigma3}, 12))
> prior({B4}, t({beta4}, {sigma4}, 12))
> prior({sigma2}{sigma3}{sigma4}, igamma(0.1, 0.1) split)
> prior({beta2}{beta3}{beta4}, normal(0, 100) split)
> block({beta2}{sigma2})
> block({beta3}{sigma3}) block({beta4}{sigma4})
> init({beta2}{beta3}{beta4} rnormal(1, 1)
> {sigma2}{sigma3}{sigma4} 1)
> burnin(5000) rseed(17)
. bayesstats summary (r2:exp(2.1*{beta2}))
> (r3:exp(2.1*{beta3})) (r4:exp(2.1*{beta4}))
Posterior summary statistics MCMC sample size = 10,000
r2 : exp(2.1* { beta2 } )
r3 : exp(2.1* { beta3 } )
r4 : exp(2.1* { beta4 } )
------------------------------------------------------------------------------
| Equal-tailed
| Mean Std. dev. MCSE Median [95% cred. interval]
-------------+----------------------------------------------------------------
r2 | 1.068262 .1032594 .00325 1.061218 .8759179 1.302069
r3 | 1.414598 .15648 .005184 1.40231 1.14427 1.765012
r4 | .7024785 .0725748 .001915 .6985938 .574165 .8566458
------------------------------------------------------------------------------
I also fit a model with normal priors for the random slopes.
. quietly bayesmh ytotal, noconstant likelihood(llf(
> yba11*{mu2:}+yba2*{mu3:}+ydelta*{mu4:} -
> ytotal*ln(1+exp({mu2:})+exp({mu3:})+exp({mu4:}))))
> define(mu2: A2[country] B2[country]#c.day, noconstant)
> define(mu3: A3[country] B3[country]#c.day, noconstant)
> define(mu4: A4[country] B4[country]#c.day, noconstant)
> prior({A2}, normal(0, 100))
> prior({A3}, normal(0, 100))
> prior({A4}, normal(0, 100))
> prior({B2}, normal({beta2}, {sigma2}))
> prior({B3}, normal({beta3}, {sigma3}))
> prior({B4}, normal({beta4}, {sigma4}))
> prior({sigma2}{sigma3}{sigma4}, igamma(0.1, 0.1) split)
> prior({beta2}{beta3}{beta4}, normal(0, 100) split)
> block({beta2}{sigma2}{beta3}{sigma3}{beta4}{sigma4},
> split gibbs)
> init({beta2}{beta3}{beta4} rnormal(1, 1)
> {sigma2}{sigma3}{sigma4} 1) rseed(17)
. bayesstats summary (r2:exp(2.1*{beta2}))
> (r3:exp(2.1*{beta3})) (r4:exp(2.1*{beta4}))
Posterior summary statistics MCMC sample size = 10,000
r2 : exp(2.1* { beta2 } )
r3 : exp(2.1* { beta3 } )
r4 : exp(2.1* { beta4 } )
------------------------------------------------------------------------------
| Equal-tailed
| Mean Std. dev. MCSE Median [95% cred. interval]
-------------+----------------------------------------------------------------
r2 | 1.066153 .1080605 .001081 1.061309 .8664183 1.292496
r3 | 1.405522 .159427 .010062 1.39786 1.120683 1.746765
r4 | .7089474 .075455 .000755 .7048609 .5734278 .8714144
------------------------------------------------------------------------------
As evident from the summaries, there are no substantive changes in the reproduction number estimates, which shows that our initial model is robust to the prior specification of random slopes.
As we saw above, the reproduction number estimates for the Philippines have high variability because of the smaller sample. It is interesting to check how these estimates change after excluding the Philippines from the estimation sample.
. quietly bayesmh ytotal if country != 6, noconstant likelihood(llf(
> yba11*{mu2:}+yba2*{mu3:}+ydelta*{mu4:} -
> ytotal*ln(1+exp({mu2:})+exp({mu3:})+exp({mu4:}))))
> define(mu2: A2[country] B2[country]#c.day, noconstant)
> define(mu3: A3[country] B3[country]#c.day, noconstant)
> define(mu4: A4[country] B4[country]#c.day, noconstant)
> prior({A2}, normal(0, 100))
> prior({A3}, normal(0, 100))
> prior({A4}, normal(0, 100))
> prior({B2}, t({beta2}, {sigma2}, 6))
> prior({B3}, t({beta3}, {sigma3}, 6))
> prior({B4}, t({beta4}, {sigma4}, 6))
> prior({sigma2}{sigma3}{sigma4}, igamma(0.1, 0.1) split)
> prior({beta2}{beta3}{beta4}, normal(0, 100) split)
> block({beta2}{sigma2})
> block({beta3}{sigma3}) block({beta4}{sigma4})
> init({sigma2}{sigma3}{sigma4} 1)
> burnin(5000) rseed(17)
. bayesstats summary (rba11:exp(2.1*{beta2}))
> (rba2:exp(2.1*{beta3})) (rdelta:exp(2.1*{beta4}))
Posterior summary statistics MCMC sample size = 10,000
rba11 : exp(2.1* { beta2 } )
rba2 : exp(2.1* { beta3 } )
rdelta : exp(2.1* { beta4 } )
------------------------------------------------------------------------------
| Equal-tailed
| Mean Std. dev. MCSE Median [95% cred. interval]
-------------+----------------------------------------------------------------
rba11 | 1.101936 .1422373 .006638 1.089014 .8338979 1.415828
rba2 | 1.313135 .1978823 .006081 1.302977 .9514345 1.731837
rdelta | .7242147 .1055362 .010449 .7109377 .5368485 .9596856
------------------------------------------------------------------------------
Now the posterior estimates for the 3 relative reproduction numbers all get closer to 1. In particular, the reproduction of BA.2 in comparison with BA.1.1, in terms of posterior mean, drops from 1.4 to 1.3, thus suggesting more moderate increase in transmissibility. In addition, the 95% credible intervals for the relative reproduction of both BA.1.1 and BA.2 now include 1.
Reference
Yamasoba, D., I. Kimura, H. Nasser, Y. Morioka, N. Nao, J. Ito, K. Uriu, et al. 2022. Virological characteristics of SARS-CoV-2 BA.2 variant. https://doi.org/10.1101/2022.02.14.480335.