Bayesian inference using multiple Markov chains
Overview
Markov chain Monte Carlo (MCMC) is the principal tool for performing Bayesian inference. MCMC is a stochastic procedure that utilizes Markov chains simulated from the posterior distribution of model parameters to compute posterior summaries and make predictions. Given its stochastic nature and dependence on initial values, verifying Markov chain convergence can be difficult—visual inspection of the trace and autocorrelation plots are often used. A more formal method for checking convergence relies on simulating and comparing results from multiple Markov chains; see, for example, Gelman and Rubin (1992) and Gelman et al. (2013). Using multiple chains, rather than a single chain, makes diagnosing convergence easier.
As of Stata 16, bayesmh and its bayes prefix commands support a new option, nchains(), for simulating multiple Markov chains. There is also a new convergence diagnostic command, bayesstats grubin. All Bayesian postestimation commands now support multiple chains. In this blog post, I show you how to check MCMC convergence and improve your Bayesian inference using multiple chains through a series of examples. I also show you how to speed up your sampling by running multiple Markov chains in parallel.
A social science case study
I present an example from social sciences concerning the social conduct of chimpanzees (Silk et al. 2005). It starts with the observation that humans, being prosocial species, are willing to cooperate and help others even at the expense of some incurring costs. The study in question investigated the cooperative behavior of primates and compared it with that of humans. The subjects in the study, chimpanzees, were given the opportunity to deliver benefits to other, unrelated, subjects at no personal costs. Their behavior was observed in two different settings, with and without the presence of another subject, and their reactions were compared. The study found that chimpanzees, in contrast to humans, did not take advantage of the opportunity to deliver benefits to other unrelated chimpanzees.
In the following example, we replicate some of the analysis in the study. The experimental data contain 504 observations. The experiment is detailed in Silk et al. (2005) and 10.1.1 in McElreath (2016). The data are available at the author repository accompanying McElreath’s (2016) book. Each chimpanzee in the experiment is seated on a table with two levers, one on the left and one on the right. There are two trays attached to each lever. The proximal trays always contain food. One of the distant trays (left or right) contains extra food, allowing the subject to share it with another chimpanzee. The response variable, pulled_left, is a binary variable indicating whether the chimpanzee pulled the left or the right lever. The predictor variables are prosoc_left, indicating whether the extra food is available on the left or on the right side of the table, and condition, indicating whether another chimpanzee is seated opposite to the subject. We expect that prosocial chimpanzees will tend to pull the left lever whenever prosoc_left and condition are both 1.
. use http://www.stata.com/users/nbalov/blog/chimpanzees.dta (Chimpanzee prosocialty experiment data)
To assess chimpanzees’ response, I model the pulled:_left variable by the predictor variable prosoc_left and the interaction between prosoc_left and condition using a Bayesian logistic regression model. The latter interaction term holds the answer to the main study question of whether chimpanzees are prosocial in the way humans are.
Fitting a model with multiple chains
The original logistic regression model considered in McElreath (2016), 10.1, is
$$
{\tt pulled\_left} \sim {\tt logit}(a + ({\tt bp} + {\tt bpC} \times {\tt condition}) \times {\tt prosoc\_left})
$$
To fit this model, I use the bayes: prefix with the following logit specification:
logit pulled_left 1.prosoc_left 1.prosoc_left#1.condition
I apply the normal(0, 100) prior for the regression coefficients, which is fairly uninformative given the binary nature of the covariates. To simulate 3 chains of length 10,000, I need to add only the nchains(3) option.
. bayes, prior({pulled_left:}, normal(0, 100)) nchains(3) rseed(16): ///
logit pulled_left 1.prosoc_left 1.prosoc_left#1.condition
Chain 1
Burn-in ...
Simulation ...
Chain 2
Burn-in ...
Simulation ...
Chain 3
Burn-in ...
Simulation ...
Model summary
------------------------------------------------------------------------------
Likelihood:
pulled_left ~ logit(xb_pulled_left)
Priors:
{pulled_left:1.prosoc_left} ~ normal(0,100) (1)
{pulled_left:1.prosoc_left#1.condition} ~ normal(0,100) (1)
{pulled_left:_cons} ~ normal(0,100) (1)
------------------------------------------------------------------------------
(1) Parameters are elements of the linear form xb_pulled_left.
Bayesian logistic regression Number of chains = 3
Random-walk Metropolis-Hastings sampling Per MCMC chain:
Iterations = 12,500
Burn-in = 2,500
Sample size = 10,000
Number of obs = 504
Avg acceptance rate = .243
Avg efficiency: min = .06396
avg = .07353
max = .0854
Avg log marginal-likelihood = -350.5063 Max Gelman-Rubin Rc = 1.001
------------------------------------------------------------------------------
| Equal-tailed
pulled_left | Mean Std. Dev. MCSE Median [95% Cred. Interval]
-------------+----------------------------------------------------------------
1.prosoc_l~t | .6322682 .2278038 .005201 .6278013 .1925016 1.078073
|
prosoc_left#|
condition |
1 1 | -.1156446 .2674704 .005786 -.1126552 -.629691 .4001958
|
_cons | .0438947 .1254382 .002478 .0448557 -.2092907 .2914614
------------------------------------------------------------------------------
Note: Default initial values are used for multiple chains.
For the purpose of later model comparison, I will save the estimation results of the current model as model1.
. bayes, saving(model1) note: file model1.dta saved . estimates store model1
Diagnosing convergence using Gelman–Rubin Rc statistics
For multiple chains, the output table includes the maximum of the Gelman–Rubin Rc statistic across parameters. The Rc statistic is used for accessing convergence by measuring the discrepancy between chains. The convergence is assessed by comparing the estimated between-chains and within-chain variances for each model parameter. Large differences between these variances indicate nonconvergence. See Gelman and Rubin (1992) and Brooks and Gelman (1998) for the detailed description of the method.
If all chains are in agreement, the maximum Rc will be close to 1. Values greater than 1.1 indicate potential nonconveregence. In our case, as evident by the low maximum Rc of 1.001, and sufficient sampling efficiency, about 8% on average, the 3 Markov chains are in agreement and converged.
The bayesstats grubin command computes and provides a detailed report of Gelman–Rubin statistics for all model parameters.
. bayesstats grubin
Gelman-Rubin convergence diagnostic
Number of chains = 3
MCMC size, per chain = 10,000
Max Gelman-Rubin Rc = 1.001097
---------------------------------
| Rc
----------------------+----------
pulled_left |
1.prosoc_left | 1.000636
|
prosoc_left#condition |
1 1 | 1.000927
|
_cons | 1.001097
---------------------------------
Convergence rule: Rc < 1.1
Given that the maximum Rc is less than 1.1, all parameter-specific Rc satisfy this convergence criterion. bayesstats grubin is useful for identifying parameters that have difficulty converging when the maximum Rc reported by bayes is greater than 1.1.
Posterior summaries using multiple chains
All Bayesian postestimation commands support multiple chains. By default, all available chains are used to compute the results. It is thus important to check the convergence of all chains before proceeding with posterior summaries and tests.
Let’s consider the odds ratio associated with the interaction between prosoc_left and condition. We can inspect it by exponentiating the corresponding parameter {pulled_left:1.prosoc_left#1.condition}.
. bayesstats summary (OR:exp({pulled_left:1.prosoc_left#1.condition}))
Posterior summary statistics Number of chains = 3
MCMC sample size = 30,000
OR : exp({pulled_left:1.prosoc_left#1.condition})
------------------------------------------------------------------------------
| Equal-tailed
| Mean Std. Dev. MCSE Median [95% Cred. Interval]
-------------+----------------------------------------------------------------
OR | .9264098 .2488245 .005092 .8909225 .5277645 1.504697
------------------------------------------------------------------------------
The posterior mean estimate of the odds ratio, 0.93, is close to 1, with a wide 95% credible interval between 0.53 and 1.50. This implies insignificant effect for the interaction between prosoc_left and condition.
The bayesstats summary command provides the sepchains option to compute posterior summaries separately for each chain and the chains() option to specify which chains are to be used for aggregating simulation results.
. bayesstats summary (exp({pulled_left:1.prosoc_left#1.condition})), sepchains
Posterior summary statistics
Chain 1 MCMC sample size = 10,000
------------------------------------------------------------------------------
| Equal-tailed
| Mean Std. Dev. MCSE Median [95% Cred. Interval]
-------------+----------------------------------------------------------------
expr1 | .9286095 .2479656 .008802 .8947938 .5258053 1.507763
------------------------------------------------------------------------------
Chain 2 MCMC sample size = 10,000
------------------------------------------------------------------------------
| Equal-tailed
| Mean Std. Dev. MCSE Median [95% Cred. Interval]
-------------+----------------------------------------------------------------
expr1 | .9243135 .250663 .009062 .8864135 .524473 1.515751
------------------------------------------------------------------------------
Chain 3 MCMC sample size = 10,000
------------------------------------------------------------------------------
| Equal-tailed
| Mean Std. Dev. MCSE Median [95% Cred. Interval]
-------------+----------------------------------------------------------------
expr1 | .9263063 .2478442 .00861 .8897752 .5357232 1.500539
------------------------------------------------------------------------------
As expected, the 3 chains produce very similar results. To demonstrate the chains() option, I now request posterior summaries for the first and the third chains combined:
. bayesstats summary (exp({pulled_left:1.prosoc_left#1.condition})), chains(1 3)
Posterior summary statistics Number of chains = 2
Chains: 1 3 MCMC sample size = 20,000
expr1 : exp({pulled_left:1.prosoc_left#1.condition})
------------------------------------------------------------------------------
| Equal-tailed
| Mean Std. Dev. MCSE Median [95% Cred. Interval]
-------------+----------------------------------------------------------------
expr1 | .9274579 .2478979 .006155 .8917017 .5326102 1.501593
------------------------------------------------------------------------------
An alternative way to estimate the effect of the interaction between prosoc_left and condition is to calculate the posterior probability of {pulled_left:1.prosoc_left#1.condition} on both sides of 0. For instance, I can use the bayestest interval command to compute the posterior probability that the interaction parameter is greater than 0.
. bayestest interval {pulled_left:1.prosoc_left#1.condition}, lower(0)
Interval tests Number of chains = 3
MCMC sample size = 30,000
prob1 : {pulled_left:1.prosoc_left#1.con
dition} > 0
-----------------------------------------------
| Mean Std. Dev. MCSE
-------------+---------------------------------
prob1 | .3371667 0.47277 .0092878
-----------------------------------------------
The estimated posterior probability is about 0.34, impyling that the posterior distribution of the interaction parameter is well spread on both sides of 0. Again, this result is not in favor of the prosocial behavior in chimpanzees, thus confirming the conclusion made in the original study.
Specifying initial values for multiple chains
By default, bayes: provides its own initial values for multiple chains. These default initial values are chosen based on the prior dsitribution of the model parameters. Here I show how to provide initial values for the chains manually. For this purpose, I specify init#() options. I sample initial values from the normal(0, 100) distribution for the first chain, uniform(-10, 0) for the second chain, and uniform(0, 10) for the third chain. This way, I guarantee dispersed initial values for all regression coefficients in the model.
. bayes, prior({pulled_left:}, normal(0, 100)) ///
init1({pulled_left:} rnormal(0, 10)) ///
init2({pulled_left:} runiform(-10, 0)) ///
init3({pulled_left:} runiform(0, 10)) ///
nchains(3) rseed(16): ///
logit pulled_left 1.prosoc_left 1.prosoc_left#1.condition
Chain 1
Burn-in ...
Simulation ...
Chain 2
Burn-in ...
Simulation ...
Chain 3
Burn-in ...
Simulation ...
Model summary
------------------------------------------------------------------------------
Likelihood:
pulled_left ~ logit(xb_pulled_left)
Priors:
{pulled_left:1.prosoc_left} ~ normal(0,100) (1)
{pulled_left:1.prosoc_left#1.condition} ~ normal(0,100) (1)
{pulled_left:_cons} ~ normal(0,100) (1)
------------------------------------------------------------------------------
(1) Parameters are elements of the linear form xb_pulled_left.
Bayesian logistic regression Number of chains = 3
Random-walk Metropolis-Hastings sampling Per MCMC chain:
Iterations = 12,500
Burn-in = 2,500
Sample size = 10,000
Number of obs = 504
Avg acceptance rate = .2134
Avg efficiency: min = .07266
avg = .07665
max = .0817
Avg log marginal-likelihood = -350.50275 Max Gelman-Rubin Rc = 1.002
------------------------------------------------------------------------------
| Equal-tailed
pulled_left | Mean Std. Dev. MCSE Median [95% Cred. Interval]
-------------+----------------------------------------------------------------
1.prosoc_l~t | .6279298 .2267905 .004858 .6317147 .1813977 1.071113
|
prosoc_left#|
condition |
1 1 | -.1113393 .2644375 .005553 -.1154978 -.6391051 .4085912
|
_cons | .0452882 .1248017 .002521 .0441162 -.2046756 .2821089
------------------------------------------------------------------------------
Note: Default initial values are used for multiple chains.
I can inspect the used initial values for the 3 chains by recalling bayes with the initsummary option.
. bayes, initsummary notable nomodelsummary
Initial values:
Chain 1: {pulled_left:1.prosoc_left} -9.83163
{pulled_left:1.prosoc_left#1.condition} .264567 {pulled_left:_cons} 4.42752
Chain 2: {pulled_left:1.prosoc_left} -4.33844
{pulled_left:1.prosoc_left#1.condition} -5.94807 {pulled_left:_cons} -7.85824
Chain 3: {pulled_left:1.prosoc_left} 3.38244
{pulled_left:1.prosoc_left#1.condition} 5.35984 {pulled_left:_cons} 3.44894
Bayesian logistic regression Number of chains = 3
Random-walk Metropolis-Hastings sampling Per MCMC chain:
Iterations = 12,500
Burn-in = 2,500
Sample size = 10,000
Number of obs = 504
Avg acceptance rate = .2134
Avg efficiency: min = .07266
avg = .07665
max = .0817
Avg log marginal-likelihood = -350.50275 Max Gelman-Rubin Rc = 1.002
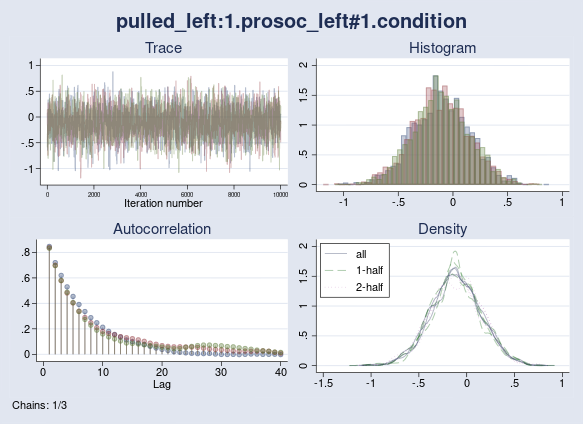
Let’s check the convergence of the interaction between prosoc_left and condition graphically. I use the bayesgraph diagnostics command.
. bayesgraph diagnostics {pulled_left:1.prosoc_left#1.condition}
As we see, all chains mix well and exhibit similar autocorrelation and density plots. We do not have convergence concerns here, which is also supported by the maximum Rc of 1.002 (< 1.1) from the previous output.
When initial values disagree with the priors
To illustrate the effect of initial values on convergence, I run the model using random initial values drawn from the uniform(-100,-50) distribution, which strongly disagrees with the prior distribution of the regression parameters. I use the initall() option to apply the same initialization (sampling from the uniform(-100, -50) distribution) to all chains.
. bayes, prior({pulled_left:}, normal(0, 100)) ///
initall({pulled_left:} runiform(-100, -50)) ///
nchains(3) rseed(16) initsummary: ///
logit pulled_left 1.prosoc_left 1.prosoc_left#1.condition
Chain 1
Burn-in ...
Simulation ...
Chain 2
Burn-in ...
Simulation ...
Chain 3
Burn-in ...
Simulation ...
Model summary
------------------------------------------------------------------------------
Likelihood:
pulled_left ~ logit(xb_pulled_left)
Priors:
{pulled_left:1.prosoc_left} ~ normal(0,100) (1)
{pulled_left:1.prosoc_left#1.condition} ~ normal(0,100) (1)
{pulled_left:_cons} ~ normal(0,100) (1)
------------------------------------------------------------------------------
(1) Parameters are elements of the linear form xb_pulled_left.
Initial values:
Chain 1: {pulled_left:1.prosoc_left} -58.6507
{pulled_left:1.prosoc_left#1.condition} -95.4699 {pulled_left:_cons} -69.8725
Chain 2: {pulled_left:1.prosoc_left} -71.6922
{pulled_left:1.prosoc_left#1.condition} -79.7403 {pulled_left:_cons} -89.2912
Chain 3: {pulled_left:1.prosoc_left} -83.0878
{pulled_left:1.prosoc_left#1.condition} -73.2008 {pulled_left:_cons} -82.7553
Bayesian logistic regression Number of chains = 3
Random-walk Metropolis-Hastings sampling Per MCMC chain:
Iterations = 12,500
Burn-in = 2,500
Sample size = 10,000
Number of obs = 504
Avg acceptance rate = .2308
Avg efficiency: min = .04952
avg = .05114
max = .05339
Avg log marginal-likelihood = -350.48911 Max Gelman-Rubin Rc = 1.15
------------------------------------------------------------------------------
| Equal-tailed
pulled_left | Mean Std. Dev. MCSE Median [95% Cred. Interval]
-------------+----------------------------------------------------------------
1.prosoc_l~t | .6805637 .2521363 .006541 .6655285 .2265225 1.189635
|
prosoc_left#|
condition |
1 1 | -.1545551 .273977 .006846 -.1557829 -.700246 .3686061
|
_cons | .0272796 .1324386 .003403 .0262892 -.233117 .2766306
------------------------------------------------------------------------------
Note: Default initial values are used for multiple chains.
Note: There is a high autocorrelation after 500 lags in at least one of the
chains.
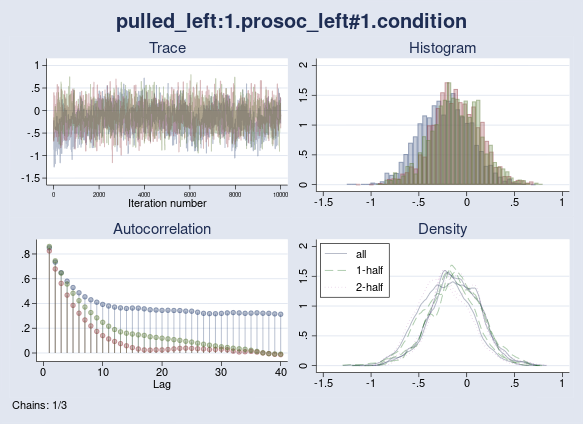
The maximum Rc is now 1.15 and is higher than the 1.1 threshold. I also see a high autocorrelation warning issued by the bayes:logit command. Lack of convergence is confirmed by the diagnostic plot of {pulled_left:1.prosoc_left} parameter, which exhibits a random-walk trace plot and high autocorrelation for one of the chains.
. bayesgraph diagnostics {pulled_left:1.prosoc_left#1.condition}
Ultimately, I can still achieve convergence if I increase the burn-in period of the chains so they all settle in the high-probability domain of the posterior distribution. The point I want to make is that once you start manipulating initial values, the default sampling settings may need to be adjusted as well.
Random-intercept model with bayesmh
I can further elaborate the logistic regression model by including random-intercept coefficients for each individual chimpanzee as identified by the actor variable. I could fit this model using bayes: melogit, but for greater flexibility in specifying priors for random effects, I will use the bayesmh command instead. I will also use nonlinear specification for the regression component in the likelihood to match the exact specification used in McElreath (2016), 10.1.1. In the new model specification, the interaction between prosoc_left and condition is given by parameter bpC. The prior for the random intercepts {actors:i.actor} is normal with mean parameter {actor} and variance {sigma2_actor}. The latter is assigned an igamma(1, 1) hyperprior.
. bayesmh pulled_left = ({actors:}+({bp}+{bpC}*condition)*prosoc_left), ///
redefine(actors:ibn.actor) likelihood(logit) ///
prior({actors:i.actor}, normal({actor}, {sigma2_actor})) ///
prior({actor bp bpC}, normal(0, 100)) ///
prior({sigma2_actor}, igamma(1, 1)) ///
block({sigma2_actor}) nchains(3) rseed(101) dots
Chain 1
Burn-in 2500 aaaaaaaaa1000aaaaaaaaa2000aa... done
Simulation 10000 .........1000.........2000.........3000.........4000........
> .5000.........6000.........7000.........8000.........9000.........10000 done
Chain 2
Burn-in 2500 aaaaaaaaa1000aaaaaaaaa2000aaaaa done
Simulation 10000 .........1000.........2000.........3000.........4000........
> .5000.........6000.........7000.........8000.........9000.........10000 done
Chain 3
Burn-in 2500 aaaaaaaaa1000aaaaaaaaa2000aaaaa done
Simulation 10000 .........1000.........2000.........3000.........4000........
> .5000.........6000.........7000.........8000.........9000.........10000 done
Model summary
------------------------------------------------------------------------------
Likelihood:
pulled_left ~ logit(xb_actors+({bp}+{bpC}*condition)*prosoc_left)
Priors:
{actors:i.actor} ~ normal({actor},{sigma2_actor}) (1)
{bp bpC} ~ normal(0,100)
Hyperpriors:
{actor} ~ normal(0,100)
{sigma2_actor} ~ igamma(1,1)
------------------------------------------------------------------------------
(1) Parameters are elements of the linear form xb_actors.
Bayesian logistic regression Number of chains = 3
Random-walk Metropolis-Hastings sampling Per MCMC chain:
Iterations = 12,500
Burn-in = 2,500
Sample size = 10,000
Number of obs = 504
Avg acceptance rate = .3336
Avg efficiency: min = .03179
avg = .04926
max = .07257
Avg log marginal-likelihood = -283.00602 Max Gelman-Rubin Rc = 1.005
------------------------------------------------------------------------------
| Equal-tailed
| Mean Std. Dev. MCSE Median [95% Cred. Interval]
-------------+----------------------------------------------------------------
bp | .8250987 .2634764 .006958 .8253262 .3170529 1.351217
bpC | -.135104 .2896624 .006208 -.1332311 -.6942856 .4007747
actor | .3816366 .845064 .023025 .3478235 -1.207322 2.170198
sigma2_actor | 4.650094 3.831105 .124065 3.511577 1.149783 15.3841
------------------------------------------------------------------------------
Note: Default initial values are used for multiple chains.
I save the estimation results of the new model as model2.
. bayesmh, saving(model2) note: file model2.dta saved . estimates store model2
Now, I can compare the two models using the bayesstats ic command.
. bayesstats ic model1 model2
Bayesian information criteria
---------------------------------------------------------
| Chains Avg DIC Avg log(ML) log(BF)
-------------+-------------------------------------------
model1 | 3 682.3504 -350.5063 .
model2 | 3 532.2629 -283.0060 67.5003
---------------------------------------------------------
Note: Marginal likelihood (ML) is computed using
Laplace-Metropolis approximation.
Because both models have 3 chains, the command reports the average DIC and log-marginal likelihood across chains. The random-intercept model is decidedly better with respect to both Avg DIC and log(BF) criteria. Employing the better-fitting model, however, does not change the insignificance of the interaction term bpC as measured by the posterior probability on the right side of 0.
. bayestest interval {bpC}, lower(0)
Interval tests Number of chains = 3
MCMC sample size = 30,000
prob1 : {bpC} > 0
-----------------------------------------------
| Mean Std. Dev. MCSE
-------------+---------------------------------
prob1 | .3227 0.46752 .0094796
-----------------------------------------------
Running chains in parallel
When you use the nchains() option wth bayesmh or bayes:, the chains are simulated sequentially, and the overall simulation time is thus proportional to the number of chains. Conditionally on the initial values, however, the chains are independent samples and can in principle be simulated in parallel. For perfect parallelization, multiple chains can be simulated in the time needed to simulate just one chain.
The unofficial command bayesparallel allows multiple chains to be simulated in parallel. You can install the command using net install.
. net install bayesparallel, from("http://www.stata.com/users/nbalov")
bayesparallel is a prefix command that can be applied to bayesmh and bayes:. bayesparallel implements parallelization by running multiple instances of Stata as separate processes. It has one notable option, nproc(#), to select the number of parallel processes to be used for simulation. The default value is 4, nproc(4). For more user control, the command also provides the stataexe() option for specifying the path to the Stata executable file. For full description of the command, see the help file:
. help bayesparallel
Let’s rerun model1 using bayesparallel. I specify the nproc(3) option so that all 3 chains are executed in parallel.
. bayesparallel, nproc(3): ///
bayes, prior({pulled_left:}, normal(0, 100)) nchains(3) rseed(16): ///
logit pulled_left 1.prosoc_left 1.prosoc_left#1.condition
Simulating multiple chains ...
Done.
Because the bayesparallel command does not calculate any summary statistics, I need to recall bayes to see the results.
. bayes
Model summary
------------------------------------------------------------------------------
Likelihood:
pulled_left ~ logit(xb_pulled_left)
Priors:
{pulled_left:1.prosoc_left} ~ normal(0,100) (1)
{pulled_left:1.prosoc_left#1.condition} ~ normal(0,100) (1)
{pulled_left:_cons} ~ normal(0,100) (1)
------------------------------------------------------------------------------
(1) Parameters are elements of the linear form xb_pulled_left.
Bayesian logistic regression Number of chains = 3
Random-walk Metropolis-Hastings sampling Per MCMC chain:
Iterations = 12,500
Burn-in = 2,500
Sample size = 10,000
Number of obs = 504
Avg acceptance rate = .243
Avg efficiency: min = .06396
avg = .07353
max = .0854
Avg log marginal-likelihood = -350.5063 Max Gelman-Rubin Rc = 1.001
------------------------------------------------------------------------------
| Equal-tailed
pulled_left | Mean Std. Dev. MCSE Median [95% Cred. Interval]
-------------+----------------------------------------------------------------
1.prosoc_l~t | .6322682 .2278038 .005201 .6278013 .1925016 1.078073
|
prosoc_left#|
condition |
1 1 | -.1156446 .2674704 .005786 -.1126552 -.629691 .4001958
|
_cons | .0438947 .1254382 .002478 .0448557 -.2092907 .2914614
------------------------------------------------------------------------------
The summary results match those of the first run, where the chains were simulated sequentially, but the execution time was cut in half. On my computer running Stata/MP 16, the regular simulation time for model1 was 5.4 seconds versus 2.7 seconds for the model run with bayesparallel.
References
Brooks, S. P., and A. Gelman. 1998. General methods for monitoring convergence of iterative simulations. Journal of Computational and Graphical Statistics 7: 434–455. https://doi.org/10.1080/10618600.1998.10474787.
Gelman, A., J. B. Carlin, H. S. Stern, D. B. Dunson, A. Vehtari, and D. B. Rubin. 2013. Bayesian Data Analysis. 3rd ed. Boca Raton, FL: Chapman & Hall/CRC.
Gelman, A., and D. B. Rubin. 1992. Inference from iterative simulation using multiple sequences. Statistical Science 7: 457–511. https://doi.org/10.1214/ss/1177011136.
McElreath, R. 2016. Statistical Rethinking: A Bayesian Course with Examples in R and Stan. Boca Raton, FL: CRC Press, Taylor and Francis Group.
Silk, J. a. a. 2005. Chimpanzees are indifferent to the welfare of unrelated group members. Nature 437: 1357–1359. https://doi.org/10.1038/nature04243.