Calculating power using Monte Carlo simulations, part 5: Structural equation models
In our last four posts in this series, we showed you how to calculate power for a t test using Monte Carlo simulations, how to integrate your simulations into Stata’s power command, and how to do this for linear and logistic regression models and multilevel models. In today’s post, I’m going to show you how to estimate power for structural equation models (SEM) using simulations.
Our goal is to write a program that will calculate power for a given SEM at different sample sizes. We’ll follow the same general procedure as the previous two posts, but the way we’ll go about simulating data is a bit different. Rather than individually simulating each variable for our specified model, we’ll be simulating all our variables simultaneously from a given covariance matrix. Means for each of the variables can also be used to simulate the data if your SEM has a mean structure, such as in group analysis or growth curve analysis.
There are three ways you can obtain a covariance matrix to simulate SEM data:
- Using a covariance matrix published in a paper or other source.
- Using the reticular action model (RAM) to derive the model-implied covariance matrix using expected parameter estimates.
- Extracting the model-implied covariance matrix after performing an sem analysis in Stata either on your own pilot study data or on another data source.
The RAM method will be demonstrated at the end of this post. Extracting model-implied covariances after using the sem command will be demonstrated below. Whichever method you choose to obtain a covariance matrix to simulate from, the remainder of our procedure will be the same as in the previous two posts. We will work through the following steps:
- Obtain or derive a covariance matrix (and means, if applicable) that corresponds with your hypothesized model under the alternative hypothesis.
- Simulate a single dataset and fit the model.
- Write a program to create the datasets, fit the models, and use simulate to test the program.
- Write a program called power_cmd_simsem that allows you to run your simulations with power.
- Optional: Write a program called power_cmd_simsem_init so that you can see convergence rates for your model at different sample sizes.
We are planning a new study to evaluate the interaction effect between age and sex on health. We can use the NHANES dataset to obtain a reasonable covariance matrix from which we can simulate new data. We will define health as a latent variable measured by systolic blood pressure (bpsystol), diastolic blood pressure (bpdiast), serum cholesterol (tcresult), and serum triglyercides (tgresult). Specifically, we would like to fit the following model:
Figure 1: Path diagram of the hypothesized model
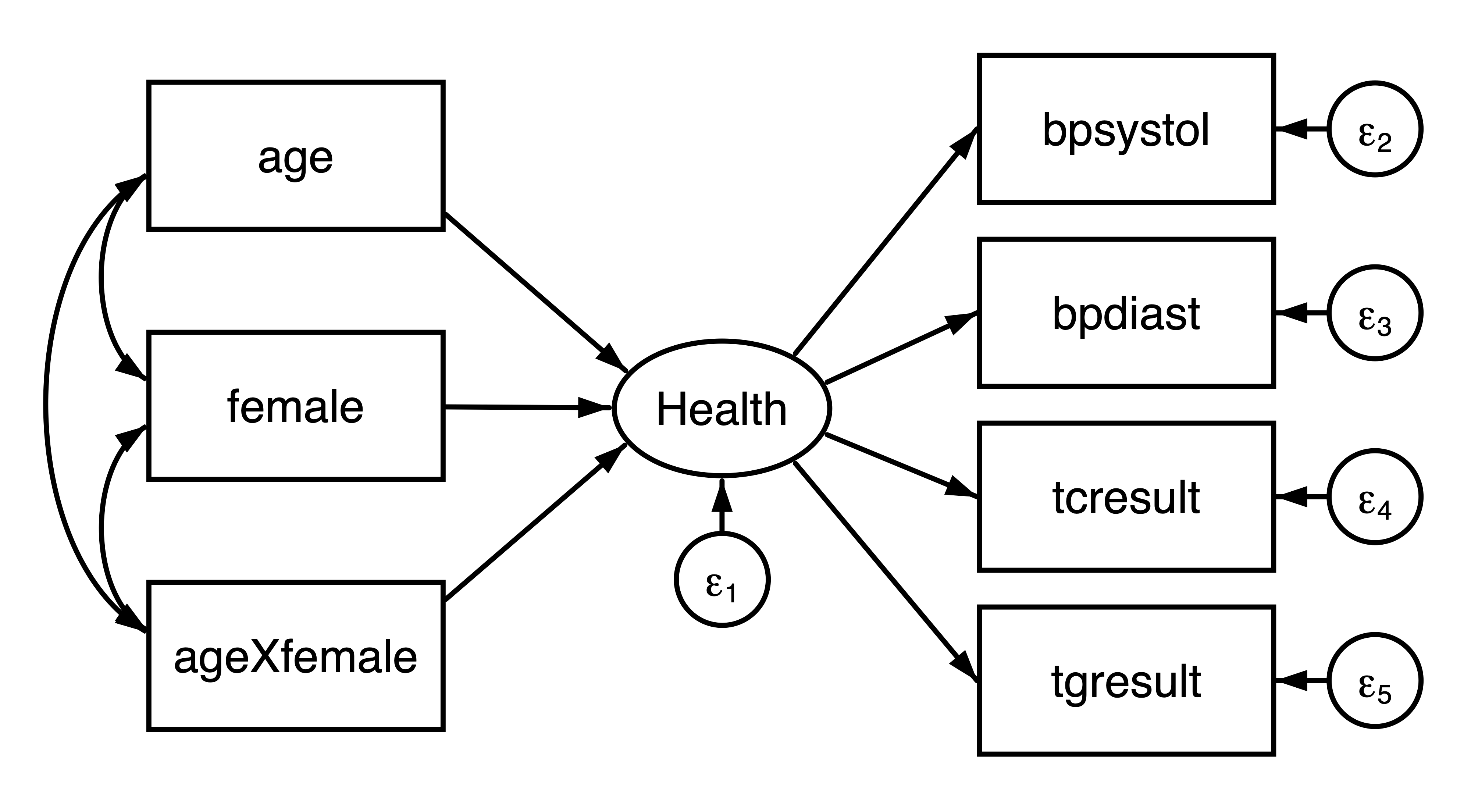
Step 1: Obtain or derive a covariance matrix (and means, if applicable) that corresponds with your hypothesized model
We are going to use the model-implied covariance matrix from fitting the above model to the NHANES data. First, we need to load the dataset, create the interaction variable, and then fit our model.
. webuse nhanes2
. gen ageXfemale = age*female
. sem (Health -> bpsystol bpdiast tcresult tgresult)
> (age female ageXfemale -> Health), nolog
(5301 observations with missing values excluded)
Endogenous variables
Measurement: bpsystol bpdiast tcresult tgresult
Latent: Health
Exogenous variables
Observed: age female ageXfemale
Structural equation model Number of obs = 5,050
Estimation method: ml
Log likelihood = -140667.36
( 1) [bpsystol]Health = 1
------------------------------------------------------------------------------
| OIM
| Coefficient std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
Structural |
Health |
age | .4371085 .0237304 18.42 0.000 .3905977 .4836193
female | -20.89331 1.67081 -12.50 0.000 -24.16804 -17.61859
ageXfemale | .3395419 .0328812 10.33 0.000 .2750961 .4039878
-------------+----------------------------------------------------------------
Measurement |
bpsystol |
Health | 1 (constrained)
_cons | 111.2516 1.207464 92.14 0.000 108.885 113.6182
-----------+----------------------------------------------------------------
bpdiast |
Health | .4404182 .0096514 45.63 0.000 .4215018 .4593346
_cons | 72.88132 .5554644 131.21 0.000 71.79263 73.97001
-----------+----------------------------------------------------------------
tcresult |
Health | .6630559 .0373398 17.76 0.000 .5898712 .7362406
_cons | 203.6104 1.217816 167.19 0.000 201.2235 205.9973
-----------+----------------------------------------------------------------
tgresult |
Health | 1.122149 .0726778 15.44 0.000 .9797029 1.264594
_cons | 123.03 2.275853 54.06 0.000 118.5694 127.4906
-------------+----------------------------------------------------------------
var(e.bpsy~l)| 67.62701 8.855679 52.31863 87.41462
var(e.bpdi~t)| 80.1877 2.164596 76.05544 84.54446
var(e.tcre~t)| 2083.505 42.75414 2001.372 2169.01
var(e.tgre~t)| 8724.877 176.5499 8385.617 9077.862
var(e.Health)| 340.7899 11.08864 319.7351 363.2312
------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(11) = 1542.14 Prob > chi2 = 0.0000
Age, sex, and their interaction are all significant predictors of Health when performed on 5,050 observations, but perhaps you don’t have the resources to collect a sample that large. How large does your sample need to be to have 80% power to detect an interaction between age and sex? To simulate data for our power analysis, we can use the model-implied covariance reported with the fitted option of the estat framework command. This will provide a lot of output, so we’ll run it quietly and just return what we’re interested in: the fitted covariance and the fitted means. Our hypothesized SEM doesn’t include mean structure, so including the means for our power analysis is unnecessary. However, I will include them in all the steps below so that our code can be generalized to other types of SEMs.
. quietly estat framework, fitted
. matrix list r(mu)
r(mu)[1,8]
Observed: Observed: Observed: Observed: Latent: Observed:
bpsystol bpdiast tcresult tgresult Health age
mu 129.84614 81.070693 215.9396 143.89584 18.594545 47.941386
Observed: Observed:
female ageXfemale
mu .51663366 24.836832
. matrix list r(Sigma)
symmetric r(Sigma)[8,8]
Observed: Observed: Observed: Observed:
bpsystol bpdiast tcresult tgresult
Observed:bpsystol 532.05333
Observed:bpdiast 204.54181 170.27163
Observed:tcresult 307.94061 135.62265 2287.6872
Observed:tgresult 521.15538 229.52632 345.55515 9309.6905
Latent:Health 464.42632 204.54181 307.94061 521.15538
Observed:age 179.49835 79.05434 119.01744 201.42383
Observed:female -1.1112203 -.48940167 -.73680119 -1.2469544
Observed:ageXfemale 64.672663 28.483019 42.881591 72.572343
Latent: Observed: Observed: Observed:
Health age female ageXfemale
Latent:Health 464.42632
Observed:age 179.49835 293.25241
Observed:female -1.1112203 .06869774 .24972332
Observed:ageXfemale 64.672663 155.35796 12.005288 729.20189
Notice that both our covariance and our means include observed as well as latent variables. We just want the information that corresponds with the observed variables, so we’ll need to extract just those portions of these matrices and save them to a new matrix. We can specify a range of rows or columns using .. between the starting and ending row or column. When concatenating matrices together, commas are used to signify a new column and backslashes (\) are used to signify a new row.
. matrix mu = r(mu)[1,1..4],r(mu)[1,6..8]
. matrix Sigma = r(Sigma)[1..4,1..4],r(Sigma)[1..4,6..8]\r(Sigma)[6..8,1..4],
> r(Sigma)[6..8,6..8]
. matrix list mu
mu[1,7]
Observed: Observed: Observed: Observed: Observed: Observed:
bpsystol bpdiast tcresult tgresult age female
mu 129.84614 81.070693 215.9396 143.89584 47.941386 .51663366
Observed:
ageXfemale
mu 24.836832
. matrix list Sigma
symmetric Sigma[7,7]
Observed: Observed: Observed: Observed:
bpsystol bpdiast tcresult tgresult
Observed:bpsystol 532.05333
Observed:bpdiast 204.54181 170.27163
Observed:tcresult 307.94061 135.62265 2287.6872
Observed:tgresult 521.15538 229.52632 345.55515 9309.6905
Observed:age 179.49835 79.05434 119.01744 201.42383
Observed:female -1.1112203 -.48940167 -.73680119 -1.2469544
Observed:ageXfemale 64.672663 28.483019 42.881591 72.572343
Observed: Observed: Observed:
age female ageXfemale
Observed:age 293.25241
Observed:female .06869774 .24972332
Observed:ageXfemale 155.35796 12.005288 729.20189
Now we have the covariance matrix and means we need to simulate our data!
Step 2: Simulate a single dataset assuming the alternative hypothesis, and fit the model
Next we create a simulated dataset from our covariance matrix (and means) using the drawnorm command. drawnorm simulates a variable or set of variables based on sample size, means, and covariance. Here we’ll use a sample size of 200.
. set seed 12345 . clear . drawnorm bpsystol bpdiast tcresult tgresult age female ageXfemale, > n(200) means(mu) cov(Sigma) (obs 200)
We can then use sem to fit the hypothesized model to our simulated data.
. sem (Health -> bpsystol bpdiast tcresult tgresult)
> (age female ageXfemale -> Health), nolog
Endogenous variables
Measurement: bpsystol bpdiast tcresult tgresult
Latent: Health
Exogenous variables
Observed: age female ageXfemale
Structural equation model Number of obs = 200
Estimation method: ml
Log likelihood = -5599.7049
( 1) [bpsystol]Health = 1
------------------------------------------------------------------------------
| OIM
| Coefficient std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
Structural |
Health |
age | .5016981 .1243038 4.04 0.000 .2580671 .7453291
female | -18.12394 8.529735 -2.12 0.034 -34.84191 -1.405964
ageXfemale | .2329537 .1611524 1.45 0.148 -.0828992 .5488066
-------------+----------------------------------------------------------------
Measurement |
bpsystol |
Health | 1 (constrained)
_cons | 111.2897 6.191827 17.97 0.000 99.15397 123.4255
-----------+----------------------------------------------------------------
bpdiast |
Health | .4507904 .0627156 7.19 0.000 .3278701 .5737107
_cons | 73.00124 3.087596 23.64 0.000 66.94967 79.05282
-----------+----------------------------------------------------------------
tcresult |
Health | .5630107 .183409 3.07 0.002 .2035357 .9224857
_cons | 207.841 6.011418 34.57 0.000 196.0588 219.6231
-----------+----------------------------------------------------------------
tgresult |
Health | .8698218 .3926678 2.22 0.027 .1002072 1.639436
_cons | 126.6153 11.5315 10.98 0.000 104.0139 149.2166
-------------+----------------------------------------------------------------
var(e.bpsy~l)| 137.2281 53.00586 64.36608 292.5695
var(e.bpdi~t)| 75.17043 12.98479 53.58117 105.4586
var(e.tcre~t)| 2235.489 226.4431 1832.949 2726.432
var(e.tgre~t)| 8917.533 902.1103 7313.681 10873.1
var(e.Health)| 303.1287 58.65825 207.4491 442.9376
------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(11) = 13.10 Prob > chi2 = 0.2866
To test the null hypothesis that the interaction term equals zero, it will be easier to conduct a Wald test using the test command with sem than using the lrtest command used in previous posts. In our case, we could have extracted the p-value from the table above, but this step can be adapted to test any hypothesis of interest.
. test ageXfemale
( 1) [Health]ageXfemale = 0
chi2( 1) = 2.09
Prob > chi2 = 0.1483
The p-value for our test is 0.148, so we would not be able to reject the null hypothesis that the interaction term equals zero.
As discussed in the previous post, the model won’t always converge when fit to simulated datasets. Like mixed, sem will store a value of 1 to e(converged) if the model converges and 0 otherwise. We will store the value of e(converged) from the model to a local macro named conv to keep track of the convergence of our models. We’ll also create a local variable, reject, that will keep track of whether the estimated interaction term is significant. The value that is stored in reject is determined by the conditional function cond(). If the model converged, then r(p)<0.05 will be evaluated. A value of 1 will be stored to reject if the Wald test p-value, r(p), is less than the alpha level, here specified as 0.05, and 0 otherwise. If the model failed to converge, then a missing value will be stored in reject.
. sem (Health -> bpsystol bpdiast tcresult tgresult) > (age female ageXfemale -> Health) . local conv = e(converged) . test ageXfemale . local reject = cond(`conv'==1, r(p)<.05, .)
Step 3: Write a program to create the datasets, fit the models, and use simulate to test the program
Next let’s write a program that creates datasets under the alternative hypothesis, fits sem models, tests the null hypothesis of interest, and uses simulate to run many iterations of the program. The primary difference between this program and the programs we have written in previous posts is that this program needs to accept matrices as input arguments. This can be a little tricky. What we need to do is specify the type of input as a string rather than a matrix. Then within the program we will define our matrices by their name, passed to the program as a string, that is, mat C = `cov’. Finally, we can use these matrices to simulate our data with drawnorm, fit our model, and test the null hypothesis. We’ve also added capture in front of the sem command to capture errors in case the model doesn’t converge. The code block below contains the syntax for this program, called simsem.
capture program drop simsem
program simsem, rclass
version 17
// PARSE INPUT
syntax, n(integer) ///
cov(string) ///
[ means(string) ///
alpha(real 0.05) ]
// COMPUTE POWER
quietly {
drop _all
mat C =`cov'
mat m = `means'
drawnorm bpsystol bpdiast tcresult tgresult age female ageXfemale, ///
n(`n') means(m) cov(C)
capture sem (Health -> bpsystol bpdiast tcresult tgresult) ///
(age female ageXfemale -> Health)
local conv = e(converged)
test ageXfemale
local reject = cond(`conv'==1, r(p)<`alpha', .)
}
// RETURN RESULTS
return scalar reject = `reject'
return scalar conv = `conv'
end
We then use simulate to run simsem 10 times using our covariance matrix and means for a sample size of 200.
. simulate reject=r(reject) converged=r(conv), reps(10) seed(12345):
> simsem, n(200) means(mu) cov(Sigma)
Command: simsem, n(200) means(mu) cov(Sigma)
reject: r(reject)
converged: r(conv)
Simulations (10)
----+--- 1 ---+--- 2 ---+--- 3 ---+--- 4 ---+--- 5
...x...x..
simulate saved two variables: reject and converged. The mean of converged is the convergence rate. The mean of reject is the power to test the null hypothesis that the age by sex interaction term equals zero.
. summarize reject
Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
reject | 8 .5 .5345225 0 1
. summarize converged
Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
converged | 10 .8 .421637 0 1
With a sample size of 200, the model converged in 8 of the 10 repetitions (80%) and had a power of 50% to detect the interaction effect on Health.
Step 4: Write a program called power_cmd_simsem, which allows you to run your simulations with power
We could stop with our quick simulation if we were interested only in a specific set of assumptions. But it’s easy to write an additional program named power_cmd_simsem that will allow us to use Stata’s power command to create tables and graphs for a range of sample sizes. We just need to include the input syntax as we did in the simsem command, simulate with the simsem command, and return the results.
capture program drop power_cmd_simsem
program power_cmd_simsem, rclass
version 17
// PARSE INPUT
syntax, n(integer) ///
cov(string) ///
[ alpha(real 0.05) ///
means(string) ///
reps(integer 100) ]
// COMPUTE POWER
quietly simulate reject=r(reject) converged=r(conv), reps(`reps'): ///
simsem, n(`n') means(`means') cov(`cov') alpha(`alpha')
// RETURN RESULTS
return scalar N = `n'
return scalar alpha = `alpha'
quietly summarize reject
return scalar power = r(mean)
quietly summarize converged
return scalar conv_rate = r(mean)
end
Step 5: (Optional) Write a program called power_cmd_simsem_init so that you can see convergence rates for your model at different sample sizes.
Convergence is often an issue in SEM simulation. If your model is having trouble converging at smaller sample sizes, it may be useful to add a convergence rate column to the power output table.
capture program drop power_cmd_simsem_init program power_cmd_simsem_init, sclass version 17 sreturn clear // ADD COLUMNS TO THE OUTPUT TABLE sreturn local pss_colnames "conv_rate" end
Using power simsem
At last, we can use power simsem to simulate power and convergence rate for a range of sample sizes. The example below simulates power for sample sizes ranging from 200 to 500, using 100 repetitions each.
. power simsem, n(200(100)500) means(mu) cov(Sigma) reps(100) > table(N conv_rate power) graph xxxxxxxxxxxxxxxxxxxxxxxxxxxxxx Estimated power Two-sided test +---------------------------+ | N conv_rate power | |---------------------------| | 200 .86 .5 | | 300 .92 .7283 | | 400 .93 .8602 | | 500 .97 .8866 | +---------------------------+
Figure 2: Estimated power for a structural equation model
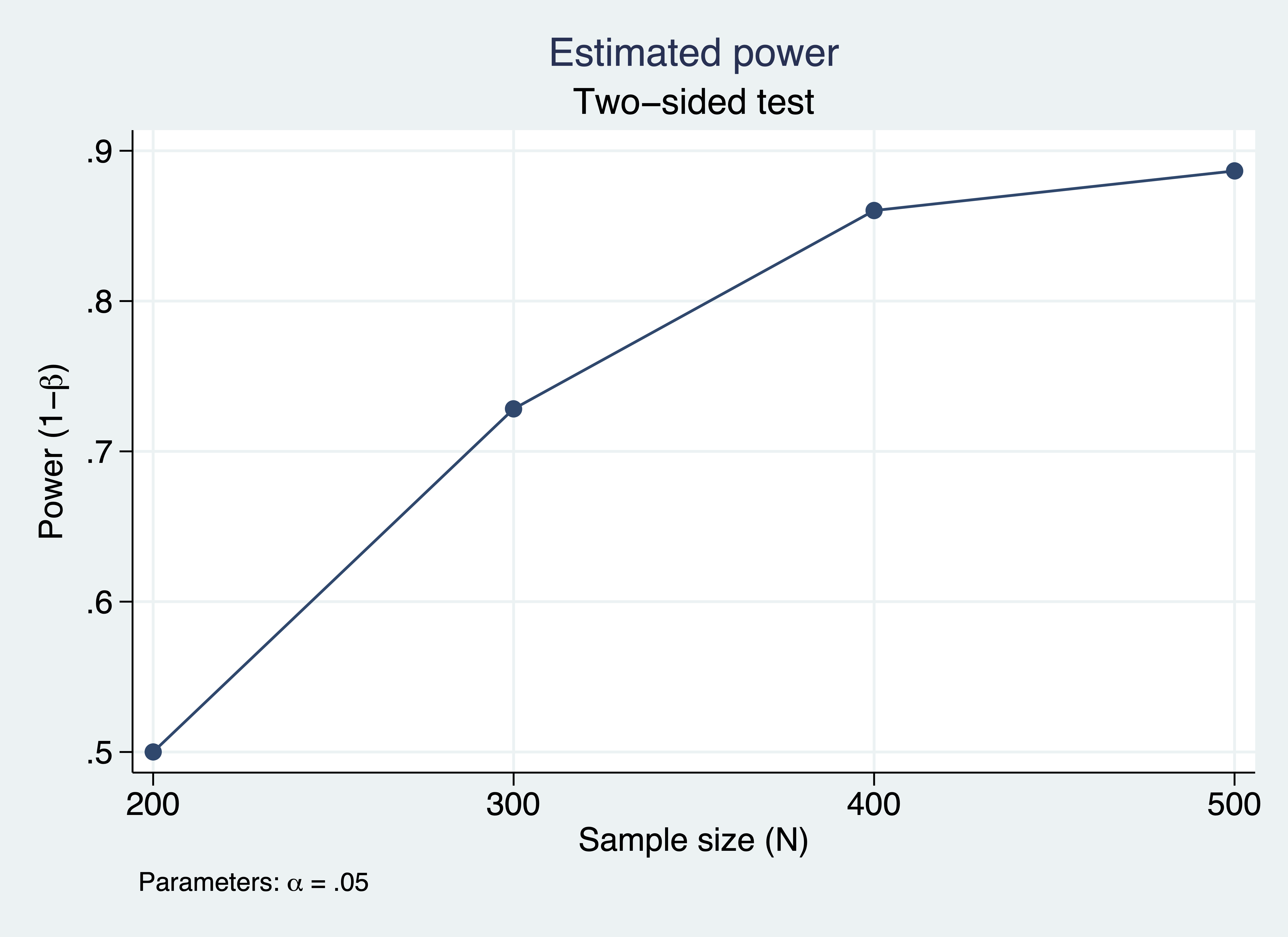
The table and graph above indicate that 80% power is achieved around a sample size of 350.
The procedure demonstrated here can be used to perform a power analysis on any SEM. You just need to define your model of interest and simulate data based on a covariance matrix. Including the previous posts in this series, we have now given examples of how you can use Stata to perform power analysis by simulation for a variety of models. You can use similar methods for virtually any power analysis you need to perform.
Deriving covariances based on SEM path coefficients using the RAM method
As discussed at the beginning of this post, you can use the RAM to directly specify population parameters or use results from a publication to obtain a covariance matrix. The RAM method uses a set of matrices to represent the model, which can be combined using matrix algebra to derive the corresponding covariance matrix. Three matrices are required: \(\mathbf{A}\), \(\mathbf{S}\), and \(\mathbf{F}\). These contain the path coefficients, factor loadings, variances, and covariances of the model you would like to simulate data from. Additionally, a matrix of means, \(\mathbf{M}\), is required if the SEM involves mean structure.
To demonstrate how to use model results to build these matrices, we will use the results from our data analysis on the NHANES datset. We will use the noxconditional option in the sem command because we need the estimated variances or covariances of the exogenous variables in order to create our matrices.
. webuse nhanes2, clear
. gen ageXfemale = age*female
. sem (Health -> bpsystol bpdiast tcresult tgresult)
> (age female ageXfemale -> Health), noxconditional nolog
(5301 observations with missing values excluded)
Endogenous variables
Measurement: bpsystol bpdiast tcresult tgresult
Latent: Health
Exogenous variables
Observed: age female ageXfemale
Structural equation model Number of obs = 5,050
Estimation method: ml
Log likelihood = -140667.36
( 1) [bpsystol]Health = 1
------------------------------------------------------------------------------
| OIM
| Coefficient std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
Structural |
Health |
age | .4371086 .0237305 18.42 0.000 .3905977 .4836194
female | -20.89331 1.67081 -12.50 0.000 -24.16804 -17.61858
ageXfemale | .3395419 .0328812 10.33 0.000 .275096 .4039878
-------------+----------------------------------------------------------------
Measurement |
bpsystol |
Health | 1 (constrained)
_cons | 111.2516 1.207464 92.14 0.000 108.885 113.6182
-----------+----------------------------------------------------------------
bpdiast |
Health | .4404182 .0096514 45.63 0.000 .4215018 .4593346
_cons | 72.88132 .5554643 131.21 0.000 71.79263 73.97001
-----------+----------------------------------------------------------------
tcresult |
Health | .6630558 .0373398 17.76 0.000 .5898711 .7362405
_cons | 203.6104 1.217816 167.19 0.000 201.2235 205.9973
-----------+----------------------------------------------------------------
tgresult |
Health | 1.122149 .0726778 15.44 0.000 .9797027 1.264594
_cons | 123.03 2.275853 54.06 0.000 118.5694 127.4906
-------------+----------------------------------------------------------------
mean(age)| 47.94139 .2409767 198.95 0.000 47.46908 48.41369
mean(female)| .5166337 .0070321 73.47 0.000 .502851 .5304163
mean(ageXf~e)| 24.83683 .3799953 65.36 0.000 24.09205 25.58161
-------------+----------------------------------------------------------------
var(e.bpsy~l)| 67.62698 8.85568 52.3186 87.41459
var(e.bpdi~t)| 80.1877 2.164596 76.05545 84.54447
var(e.tcre~t)| 2083.505 42.75414 2001.372 2169.01
var(e.tgre~t)| 8724.877 176.5499 8385.617 9077.862
var(e.Health)| 340.79 11.08864 319.7351 363.2313
var(age)| 293.2524 5.835941 282.0344 304.9166
var(female)| .2497233 .0049697 .2401704 .2596562
var(ageXfe~e)| 729.2019 14.51166 701.3071 758.2062
-------------+----------------------------------------------------------------
cov(age,|
female)| .0686977 .1204256 0.57 0.568 -.167332 .3047275
cov(age,|
ageXfemale)| 155.358 6.864694 22.63 0.000 141.9034 168.8125
cov(female,|
ageXfemale)| 12.00529 .2541636 47.23 0.000 11.50714 12.50344
------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(11) = 1542.14 Prob > chi2 = 0.0000
The first matrix we will create is the \(\mathbf{A}\) matrix. The \(\mathbf{A}\) matrix is an asymmetric matrix that stores the single-headed path coefficients in the model. The rows and columns of our matrix represent each of the observed and latent variables. The cells represent paths from the column variable to the row variable. I will start by creating a matrix of 0s of the size that I need using J(r,c,z), an \(r \times c\) matrix containing elements z. Then I will substitute blocks of cells with the paths from the model into the \(\mathbf{A}\) matrix. We only need to specify the upper left cell of the cells we are substituting. Finally, I will add row and column names to this matrix to make it easier to interpret.
. matrix A = J(8,8,0)
. matrix A[1,8] = (1.00\0.44\0.66\1.12)
. matrix A[8,5] = (0.44,-20.89,0.34)
. matrix rownames A = bpsystol bpdiast tcresult tgresult age female
> ageXfemale Health
. matrix colnames A = bpsystol bpdiast tcresult tgresult age female
> ageXfemale Health
. matrix list A
A[8,8]
bpsystol bpdiast tcresult tgresult age
bpsystol 0 0 0 0 0
bpdiast 0 0 0 0 0
tcresult 0 0 0 0 0
tgresult 0 0 0 0 0
age 0 0 0 0 0
female 0 0 0 0 0
ageXfemale 0 0 0 0 0
Health 0 0 0 0 .44
female ageXfemale Health
bpsystol 0 0 1
bpdiast 0 0 .44
tcresult 0 0 .66
tgresult 0 0 1.12
age 0 0 0
female 0 0 0
ageXfemale 0 0 0
Health -20.89 .34 0
The \(\mathbf{S}\) matrix is a symmetric matrix that stores double-headed path coefficients, variances, and covariances of our model. I start by creating a diagnal matrix of all the estimated variances from the model, and then I add the covariances of the exogenous variables.
. matrix S = diag((67.63,80.19,2083.51,8724.88,0,0,0,340.79))
. matrix S[5,5] = (293.25,0.07,155.36\0.07,0.25,12.01\155.36,12.01,729.20)
. matrix rownames S = bpsystol bpdiast tcresult tgresult age female
> ageXfemale Health
. matrix colnames S = bpsystol bpdiast tcresult tgresult age female
> ageXfemale Health
. matrix list S
symmetric S[8,8]
bpsystol bpdiast tcresult tgresult age
bpsystol 67.63
bpdiast 0 80.19
tcresult 0 0 2083.51
tgresult 0 0 0 8724.88
age 0 0 0 0 293.25
female 0 0 0 0 .07
ageXfemale 0 0 0 0 155.36
Health 0 0 0 0 0
female ageXfemale Health
female .25
ageXfemale 12.01 729.2
Health 0 0 340.79
The \(\mathbf{F}\) matrix is a rectangular matrix to distinguish observed and latent variables. The rows represent each observed variable, and the columns represent each observed and latent variable. Each row gets a `1′ in the cell of that variable’s corresponding column, creating a diagonal submatrix. A diagonal matrix of 1s is also called the identity matrix. We can specify an identity matrix with I(n) where n is the number of rows/columns. I add a column vector of 0s with J().
. matrix F = I(7),J(7,1,0)
. matrix rownames F = bpsystol bpdiast tcresult tgresult age female
> ageXfemale
. matrix colnames F = bpsystol bpdiast tcresult tgresult age female
> ageXfemale Health
. matrix list F
F[7,8]
bpsystol bpdiast tcresult tgresult age
bpsystol 1 0 0 0 0
bpdiast 0 1 0 0 0
tcresult 0 0 1 0 0
tgresult 0 0 0 1 0
age 0 0 0 0 1
female 0 0 0 0 0
ageXfemale 0 0 0 0 0
female ageXfemale Health
bpsystol 0 0 0
bpdiast 0 0 0
tcresult 0 0 0
tgresult 0 0 0
age 0 0 0
female 1 0 0
ageXfemale 0 1 0
Finally, if your model involves mean structure, an \(\mathbf{M}\) matrix must also be created to obtain the model-implied means. This is just a column vector of estimated means or intercepts for the observed and latent variables in the model. Unless explicitly estimated, you can assume all the latent variable means are 0.
. matrix M = (111.25\72.88\203.61\123.03\47.94\.52\24.84\0)
. matrix rownames M = bpsystol bpdiast tcresult tgresult age female
> ageXfemale Health
. matrix list M
M[8,1]
c1
bpsystol 111.25
bpdiast 72.88
tcresult 203.61
tgresult 123.03
age 47.94
female .52
ageXfemale 24.84
Health 0
Now we can use matrix algebra to derive the model-implied means and covariance. The dimension of I() will need to be changed based on the number of observed and latent variables in the model. Here it’s 8 to include the seven observed variables and the one latent variable.
. *model-implied means
. matrix mu = F*inv(I(8)-A)*M
. matrix list mu
mu[7,1]
c1
bpsystol 129.9264
bpdiast 81.097616
tcresult 215.93642
tgresult 143.94757
age 47.94
female .52
ageXfemale 24.84
. *model-implied covariance
. matrix Sigma = F*inv(I(8)-A)*S*inv(I(8)-A)'*F'
. matrix list Sigma
symmetric Sigma[7,7]
bpsystol bpdiast tcresult tgresult age
bpsystol 533.17918
bpdiast 204.84164 170.32032
tcresult 307.26246 135.19548 2286.3032
tgresult 521.41508 229.42264 344.13395 9308.8649
age 180.3901 79.371644 119.05747 202.03691 293.25
female -1.1083 -.487652 -.731478 -1.241296 .07
ageXfemale 65.3975 28.7749 43.16235 73.2452 155.36
female ageXfemale
female .25
ageXfemale 12.01 729.2
We see the covariance matrix implied by the model with the supplied model parameters.